【题目】已知一次函数y=kx+b的图象经过点(0,1)和(1,﹣2).
(1)求函数的解析式;
(2)求直线y=kx+b上到x轴距离为7的点的坐标.
参考答案:
【答案】(1)y=﹣3x+1;(2)直线y=kx+b上到x轴距离为7的点的坐标为(﹣2,7)或(![]() ,﹣7).
,﹣7).
【解析】
(1)利用待定系数法求一次函数解析式;
(2)分别求出函数值为7或-7对应的自变量的值即可.
(1)把(0,1),(1,-2)分别代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y=-3x+1;
(2)当y=7时,-3x+1=7,解得x=-2,此时满足条件的点的坐标为(-2,7);
当y=-7时,-3x+1=-7,解得x=![]() ,此时满足条件的点的坐标为(
,此时满足条件的点的坐标为(![]() ,-7);
,-7);
综上所述,直线y=kx+b上到x轴距离为7的点的坐标为(-2,7)或(![]() ,-7).
,-7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】田忌赛马的故事为我们熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块10、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出10时,小齐随机出牌应对,求小齐本次比赛获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.

(1)求证:△ABC∽△CBD;
(2)如果AC=4,BC=3,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
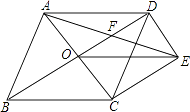
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长. -
科目: 来源: 题型:
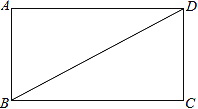
查看答案和解析>>【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O(用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:AF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.

(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
相关试题

