【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 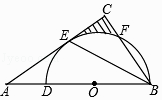
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
参考答案:
【答案】
(1)解:连接OE,
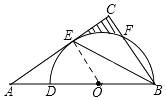
∴BE是∠OBC的角平分线,
∴∠OBE=∠CBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∵OE是⊙O的半径,
∴AC是⊙O的切线;
(2)解:连接OF,
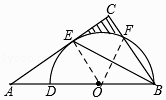
∵cosA= ![]() ,
,
∴∠A=30°,
∴∠ABC=∠AOE=60°
∵OB=OF=3,
∴∠FOB=∠ABC=60°,
∴∠EOF=60°,
∴扇形OEF的面积为: ![]() =
= ![]() ,
,
∵OE=3,∠BAC=30°,
∴AO=2OE=6,
∴AB=AO+OB=9,
∴BC= ![]() AB=
AB= ![]()
∴由勾股定理可知:AE=3 ![]() ,AC=
,AC= ![]() ,
,
∴CE=AC﹣AE= ![]() ,
,
∵BF=OB=3,
∴CF=BC﹣BF= ![]()
∴梯形OFCE的面积为: ![]() =
= ![]() ,
,
∴阴影部分面积为: ![]() ﹣
﹣ ![]()
【解析】(1)连接,根据BE平分∠OBC,OE=OB,可得出OE∥BC,从而可知∠AEO=∠C=90°,根据切线的判定,即可得出AC是⊙O的切线;(2)连接OF,根据条件分别求出OE、CF、CE,∠EOF的数值后,根据面积公式分别计算梯形OFCE与扇形EOF的面积,从而可求出阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 、
、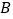 、
、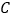 在同一条直线上,且
在同一条直线上,且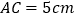 ,
,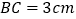 ,点
,点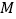 、
、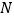 分别是
分别是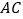 、
、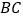 的中点.
的中点.  画出符合题意的图形;
画出符合题意的图形; 依据
依据 的图形,求线段
的图形,求线段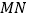 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC的边长为2,点D在射线CB上,点E在射线AC上,且AD=AE,∠EDC=15°,则线段CD=_______.
-
科目: 来源: 题型:
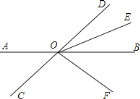
查看答案和解析>>【题目】如图,直线
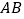 、
、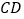 相交于点
相交于点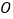 ,
,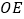 平分
平分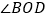 ,
,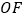 平分
平分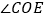 ,
,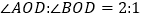
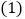 求
求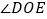 的度数;
的度数;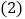 求
求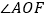 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D是AC上的一点,在BC上取一点E,使BE=CD,连接AE交BD于点P,在BD的延长线上取一点Q,使AP=PQ,连接AQ、CQ,点G为PQ的中点,DG=PE,若CQ=
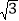 ,则BQ=________________.
,则BQ=________________.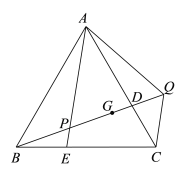
-
科目: 来源: 题型:
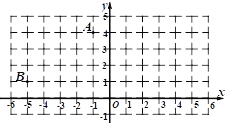
查看答案和解析>>【题目】点A(1,4)和点B(5,1)在平面直角坐标系中的位置如图所示:
(1)点A1、B1分别为点A、B关于y轴的对称点,请画出四边形AA1B1B,并写出A1、B1的坐标;
(2)在(1)的条件下,画一条过四边形AA1B1B的一个顶点的线段,将四边形AA1B1B分成两个图形,并且使分得的图形中的一个是轴对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店从机械厂购进甲、乙两种零件进行销售,若甲种零件每件的进价是乙种零件每件进价的
 ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.(1)求每件甲种零件和每件乙种零件的进价分别为多少元?
(2)若该商店计划购进甲、乙两种零件共110件,准备将零件批发给零售商. 甲种零件的批发价是每件100元,乙种零件的批发价是每件130元,该商店计划将这批产品全部售出从零售商处获利不低于3000元,那么该商店最多购进多少件甲种零件?
相关试题

