【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
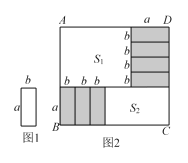
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S2-S1的值为 .
(2)当AD=40时,请用含a、b的式子表示 S2-S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2-S1 的值总保持不变,则a、b 满足的关系是 .
参考答案:
【答案】(1)630;-63;(2)40a-160b+ab;(3)a=4b
【解析】试题分析:(1)根据长方形的面积公式,直接计算即可;求出S1和S2的面积,相减即可;
(2)用含a、b的式子表示出S1和S2的面积,即可求得结论;
(3)用含a、b、AD的式子表示出S2-S1,根据S2-S1的值总保持不变,即与AD的值无关,整理后,让AD的系数为0即可.
试题解析:(1)长方形ABCD的面积为30×(4×3+9)=630;S2-S1=(30-9)×9-(30-9)×4×3=-63;
(2)S2-S1=a(30-3b)-4b(30-a)=40a-160b+ab;
(3)∵S2-S1= a(AD-3b)-4b(AD-a),
整理,得:S2-S1=(a -4b)AD+ab,
∵若AB长度不变,AD变长,而S2-S1的值总保持不变,
∴a - 4b=0,
解得:a=4b.
即a,b满足的关系是a=4b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为a的正方形的一角减去一个边长为的小正方形(a>b),如图①

① ②
(1)由图①得阴影部分的面积为 .
(2)沿图①中的虚线剪开拼成图②,则图②中阴影部分的面积为 .
(3)由(1)(2)的结果得出结论: = .
(4)利用(3)中得出的结论计算:20172-20162
-
科目: 来源: 题型:
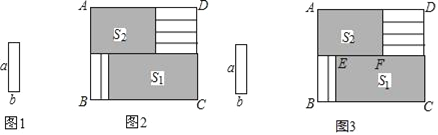
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=_________,S2=_________;
(2)求a,b满足的关系式,写出推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.
(2)如果|x+1|=3,那么x= ;
(3)若|a-3|=2,|b+2|=1,且数a、b在数轴上表示的数分别是点A、点B,则A、B 两点间的最大距离是 .
(4)若数轴上表示a的点位于-4与2之间,则|a+4|+|a-2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( ).
A.1∶2∶3∶4
B.1∶2∶2∶1
C.1∶1∶2∶2
D.2∶1∶2∶1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西省贺州市第23题)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=
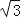 ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)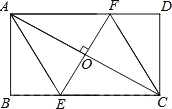
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10 台和
液晶显示器8台,共需要资金7000 元;若购进电脑机箱2台和液晶显示器5台,共需要资金
4120元.
(1)每合电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元. 根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元. 该经销商希望销售完这两种商品,所获利润不少于4100元. 试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
相关试题

