【题目】一个盒子里装有不多于![]() 颗糖,如果每次
颗糖,如果每次![]() 颗,
颗,![]() 颗,
颗,![]() 颗或
颗或![]() 颗的取出,最终盒内都只剩下一颗糖,如果每次以
颗的取出,最终盒内都只剩下一颗糖,如果每次以![]() 颗的取出,那么正好取完,则盒子里共有___颗糖.
颗的取出,那么正好取完,则盒子里共有___颗糖.
参考答案:
【答案】121
【解析】
在200以内分别找到11的倍数及24的倍数+1的数,取两组数中同时出现的数即可.
解:∵每次以11颗的取出正好取完,
∴盒子内糖数必为11的倍数,
∵盒子里装有不多于200颗糖,
∴盒子内糖数可能为11、22、33、44、55、66、77、88、99、110、121、132、143、154、165、176、187、198;
又∵如果每次2颗,3颗,4颗或6颗地取出,最终盒内都只剩一颗糖,
∴盒子内糖数为24的倍数+1,即盒子内糖数可能为25、49、73、97、121、145、169、193,
∴盒子里共有121颗糖,
故答案为:121.
-
科目: 来源: 题型:
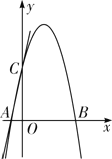
查看答案和解析>>【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F、E的坐标.
-
科目: 来源: 题型:
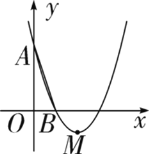
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+C经过A(0,3),B(1,0)两点,顶点为M.
(1)求b、C的值;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式;
(3)设(2)中平移所得的抛物线与y轴的交点为A1,顶点为M1,若点P在平移后的抛物线上,且满足△PMM1的面积是△PAA1面积的3倍,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=-
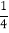 x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).(1)求该二次函数的表达式及点C的坐标;
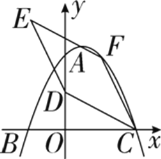
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
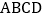 和正方形
和正方形 的顶点
的顶点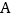 在
在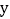 轴上,顶点
轴上,顶点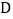 ,
,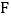 在
在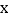 轴上,点
轴上,点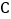 在
在 边上,反比例函数
边上,反比例函数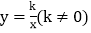 的图象经过点
的图象经过点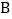 、
、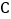 和边
和边 的中点
的中点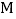 .若
.若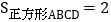 ,则正方形
,则正方形 的面积为( )
的面积为( )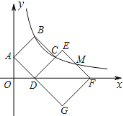
A.
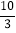 B.
B. 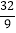 C.
C. 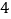 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
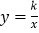 上一点
上一点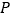 ,过
,过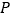 作
作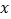 轴,
轴,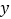 轴的垂线,垂足分别为
轴的垂线,垂足分别为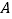 、
、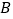 ,矩形
,矩形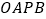 的面积为
的面积为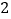 ,则双曲线与直线在
,则双曲线与直线在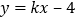 交点在第一象限内的点的坐标为________.
交点在第一象限内的点的坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某人身高
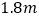 ,开始时站在路灯下的影子长为
,开始时站在路灯下的影子长为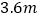 ,然后他向路灯走近
,然后他向路灯走近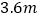 (指水平距离),此时他的影子长与身高相等.求路灯高,以及开始时他与路灯的水平距离.
(指水平距离),此时他的影子长与身高相等.求路灯高,以及开始时他与路灯的水平距离.
相关试题

