【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
参考答案:
【答案】(1)答案不唯一.如y=x2和y=2x2 (2)y2=5x2-10x+5 ,5
【解析】试题分析:
(1)由“同族二次函数的定义”可知,在二次函数的顶点式: ![]() 中,只要在两个二次函数中
中,只要在两个二次函数中![]() 分别相等,
分别相等, ![]() 取同号的不相等实数,就可得到两个“同族二次函数”;
取同号的不相等实数,就可得到两个“同族二次函数”;
(2)由![]() 的图象过点A(1,1)可求出
的图象过点A(1,1)可求出![]() 的解析式,及
的解析式,及![]() 的顶点坐标;同时可表达出
的顶点坐标;同时可表达出![]() 的解析式,再由
的解析式,再由![]() 与
与![]() 是“同族二次函数”可列出关于
是“同族二次函数”可列出关于![]() 的方程组,解方程组可求得
的方程组,解方程组可求得![]() 的值,就可得到
的值,就可得到![]() 的解析式.
的解析式.
试题解析:
(1)由“同族二次函数的定义”可知: ![]() 和
和![]() 是一对“同族二次函数”(答案不唯一);
是一对“同族二次函数”(答案不唯一);
(2)∵![]() 的图象过点A(1,1),
的图象过点A(1,1),
∴![]() ,解得:
,解得: ![]() ,
,
∴![]() ,
,
∴![]() 的顶点坐标为(1,1),且
的顶点坐标为(1,1),且![]() ,
,
∵![]() 与
与![]() 是“同族二次函数”,
是“同族二次函数”,
∴![]() 的顶点坐标也为(1,1),
的顶点坐标也为(1,1),
∴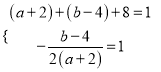 ,解得:
,解得: ![]() ,
,
∴![]() ,
,
又∵![]() 在对称轴
在对称轴![]() 的右侧,
的右侧,
∴当![]() 时,
时, ![]() 2最小=5.
2最小=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2m2﹣8= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
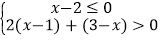 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.【答案】﹣1<x≤2,数轴表示见解析.
【解析】试题分析:分别求出不等式组中两个不等式的解集,再求出其公共解集,然后在数轴上表示出其解集.

由①得,x≤2,
由②得,x>﹣1,
故此不等式组的解集为:﹣1<x≤2.
在数轴上表示为:
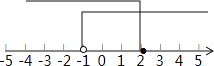
点睛: 本题考查了一元一次不等式组的解法及解集的数轴表示,先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.在数轴上空心圈表示不包含该点,实心点表示包含该点.
【题型】解答题
【结束】
22【题目】解不等式组:
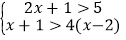 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一种细胞的直径约为0.000 052米,将0.000 052用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3a2﹣6a)÷3a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 三角形的三条中线交于一点 B. 三角形的三条高都在三角形内部
C. 三角形不一定具有稳定性 D. 三角形的角平分线可能在三角形的内部或外部
相关试题

