【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( ) 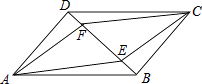
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
参考答案:
【答案】D
【解析】解:如图,连接AC与BD相交于O, 在ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选D.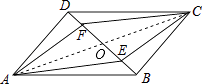
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9x﹣x3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一位同学做的四道题:①a3+a3=a6;②(xy2)3=x3y6;③x2x3=x6;④(﹣a)2÷a=﹣a.其中做对的一道题是( )
A.①
B.②
C.③
D.④ -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:﹣(﹣a2+2ab+b2)+(﹣a2﹣ab+b2),其中a=﹣
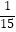 ,b=10.
,b=10. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)解不等式:2x﹣3≤ (x+2)
(x+2)
(2)解方程组: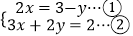 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD中,AB∥OC,BC∥AO,A、C两点的坐标分别为(﹣
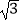 ,
, 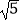 )、(﹣2
)、(﹣2 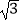 ,0),A、B两点间的距离等于O、C两点间的距离.
,0),A、B两点间的距离等于O、C两点间的距离.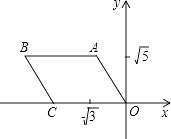
(1)点B的坐标为;
(2)将这个四边形向下平移2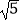 个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形四个顶点的坐标.
个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形四个顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
相关试题

