【题目】(本题9分)把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴当a=b=1时,M有最小值1
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
参考答案:
【答案】(1)4;(2)![]() ;(3)M的最小值-3;(4)a+b+c=5.
;(3)M的最小值-3;(4)a+b+c=5.
【解析】
试题(1)添加的常数项为一次项系数4一半的平方,即这个常数项为4;(2)类比例题进行分解因式即可;(3)类比例题求M的最小值即可;
试题解析:(1)4;
(2)a2-24a+143=a2-24a+144-1=![]() =(a-12+1)(a-12-1)=
=(a-12+1)(a-12-1)=![]() ;
;
(3)M=![]() a2+2a +1=
a2+2a +1=![]() a2+2a+4-3=
a2+2a+4-3=![]() ,
,
∵![]() ≥0,
≥0,
∴当a=-4时,M有最小值-3.
(4)![]()
![]() ,
,
∴![]() ,
,
解得a=1,b=2,c=2.
∴a+b+c=1+2+2=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解下列因式:
(1)
 . (2)
. (2)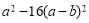 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=16 cm,点C为线段AB上的一个动点(点C不与A,B重合),点D,E分别是AC和BC的中点.
(1)求DE的长;
(2)知识迁移:如图②,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE的大小与射线OC的位置无关.
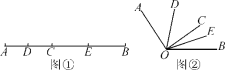
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数 1 至 1050 按一定规律排列如下表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
从表中任取一个 3 3 的方框(如表中带阴影的部分),方框中九个数的和可能是( )
A. 2025 B. 2018 C. 2016 D. 2007
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )
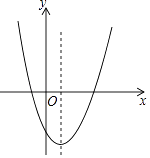
A.abc<0,b2﹣4ac>0
B.abc>0,b2﹣4ac>0
C.abc<0,b2﹣4ac<0
D.abc>0,b2﹣4ac<0 -
科目: 来源: 题型:
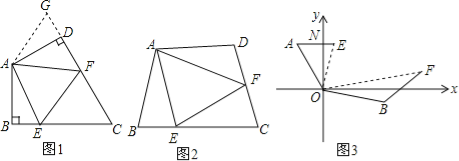
查看答案和解析>>【题目】(13分)(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=
 ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
相关试题

