Question

【题目】完成下面的证明。
已知：如图，BE∥CD，∠A＝∠1，
求证：∠C＝∠E。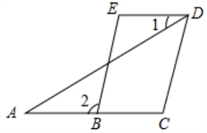

证明：∵BE∥CD （已知 ）
∴∠2=∠C （ ）
又 ∵∠A=∠1 （已知 ）
∴ AC∥DE （ ）
∴ ∠2＝∠E（ ）
∴∠C=∠E （ ）

Answer 1

【答案】证明：∵BE∥CD （已知 ）
∴∠2=∠C （ 两直线平行，同位角相等 ）
又 ∵∠A=∠1 （已知 ）
∴ AC∥DE （ 内错角相等，两直线平行 ）
∴ ∠2＝∠E（ 两直线平行，内错角相等 ）
∴∠C=∠E （ 等量代换 ）
【解析】由BE//CD 得∠2=∠C，根据是两直线平行，同位角相等；而∠1=∠A得AC∥DE，根据是内错角相等，两直线平行；再根据两直线平行，内错角相等得∠2=∠E，由等量代换 即可得到结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．