【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)详见解析;(2)30°;(3)![]() .
.
【解析】试题分析:(1)连接![]() 圆的半径相等和已知条件证明
圆的半径相等和已知条件证明![]() ,即可证明
,即可证明![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 首先证明
首先证明![]() 是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠
是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠![]() 的度数;
的度数;
(3)过点O作OG⊥AB于点G,得到AG=BG,在![]() 中
中![]() 设DE=5x,则AE=13x,AD=12x,AO=24x,把
设DE=5x,则AE=13x,AD=12x,AO=24x,把![]() 表示出来,在
表示出来,在![]() 中,用三角函数的知识列出方程,解出
中,用三角函数的知识列出方程,解出![]() 得值,即可求出半径.
得值,即可求出半径.
试题解析:(1)证明:连接OB,
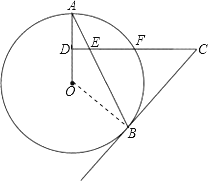
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC.
又∵CD⊥OA.
![]()
![]()
∴OB⊥BC
∴BC是![]() 的切线.
的切线.
(2)连接OF,AF,BF,
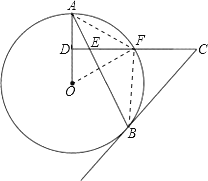
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
![]()
![]()
(3)连接OF,AF,
∵DA=
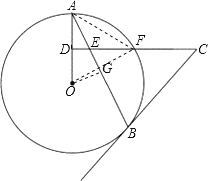
∴AF=OF=OA,
过点O作OG⊥AB于点G,得到AG=BG,
在![]() 中
中![]()
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
则![]()
又∵![]() 中,
中, ![]() 则
则![]()
则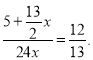
解得![]()
![]()
-
科目: 来源: 题型:
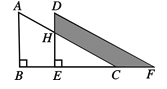
查看答案和解析>>【题目】如图,两个全等的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8, DH=2,平移距离为3,则阴影部分的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知△ABC的顶点均为网格线的交点.
(1)将△ABC向下平移5个单位长度,再向左平移1个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于直线l轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C3以A、A3、B、B3为顶点的四边形的面积为 .

相关试题

