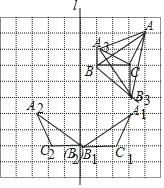
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知△ABC的顶点均为网格线的交点.
(1)将△ABC向下平移5个单位长度,再向左平移1个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于直线l轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C3以A、A3、B、B3为顶点的四边形的面积为 .

参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)作出A,B,C的对应点A1,B1,C1即可.
(2)作出A1,B1,C1的对应点A2,B2,C2即可.
(3)作出A,B的对应点A3,B3即可,利用分割法求四边形的面积即可.
解:(1)△A1B1C1;如图所示.
(2)△A2B2C2如图所示.
(3)△A3B3C3如图所示,![]()
![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=
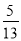 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.

(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:
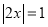 .
.解:讨论:①当
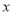 ≥0时,原方程可化为
≥0时,原方程可化为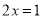 ,它的解是
,它的解是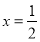 .
.②当
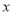 <0时,原方程可化为
<0时,原方程可化为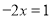 ,它的解是
,它的解是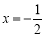 .
.∴原方程的解为
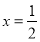 和
和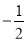 .
.问题(1):依例题的解法,方程
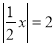 的解是 ;
的解是 ;问题(2):尝试解绝对值方程:
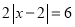 ;
;问题(3):在理解绝对值方程解法的基础上,解方程:
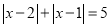 .
.
相关试题

