【题目】如图(1),有![]() 、
、![]() 、
、![]() 三种不同型号的卡片若干张,其中
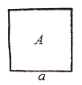
三种不同型号的卡片若干张,其中![]() 型是边长为
型是边长为![]()
![]() 的正方形,
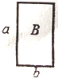
的正方形,![]() 型是长为
型是长为![]() 、宽为
、宽为![]() 的长方形,
的长方形,![]() 型是边长为
型是边长为![]() 的正方形.
的正方形.

图(1) 图(2)
(1)若用![]() 型卡片
型卡片![]() 张,
张,![]() 型卡片
型卡片![]() 张,
张,![]() 型卡片
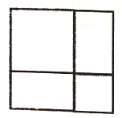
型卡片![]() 张拼成了一个正方形(如图(2)),此正方形的边长为_______,根据该图形请写出一条属于因式分解的等式:_________;
张拼成了一个正方形(如图(2)),此正方形的边长为_______,根据该图形请写出一条属于因式分解的等式:_________;
(2)若要拼一个长为![]() ,宽为
,宽为![]() 的长方形,设需要
的长方形,设需要![]() 类卡片
类卡片![]() 张,
张,![]() 类卡片
类卡片![]() 张,
张,![]() 类卡片
类卡片![]() 张,则
张,则![]() _______;
_______;
(3)现有![]() 型卡片
型卡片![]() 张,
张,![]() 型卡片
型卡片![]() 张,
张,![]() 型卡片
型卡片![]() 张,从这
张,从这![]() 张卡片中拿掉两张卡片,余下的卡片全用上,你能拼出一个长方形或正方形吗?有几种拼法?请你通过运算说明理由.
张卡片中拿掉两张卡片,余下的卡片全用上,你能拼出一个长方形或正方形吗?有几种拼法?请你通过运算说明理由.
参考答案:
【答案】(1)a+b,a2+2ab+b2=(a+b)2;(2)9;(3)(3)四种拼法,理由见解析.
【解析】
(1)由图可得可得正方形的边长为a+b,由图(2)可得因式分解的等式![]() ;
;
(2)因为![]() ,所以需要用
,所以需要用![]() 类卡片2张,
类卡片2张,![]() 类卡片5张,
类卡片5张,![]() 类卡片2张,即可求
类卡片2张,即可求![]() 、
、![]() 、
、![]() 对应的值;
对应的值;
(3)分类讨论:第一种:![]() 型卡片拿掉1张,
型卡片拿掉1张,![]() 型卡片拿掉1张,则能拼出一个长方形,即长方形的长为
型卡片拿掉1张,则能拼出一个长方形,即长方形的长为![]() ,宽为
,宽为![]() ;第二种:
;第二种:![]() 型卡片拿掉1张,
型卡片拿掉1张,![]() 型卡片拿掉1张,则能拼出一个长方形,即长方形的长为
型卡片拿掉1张,则能拼出一个长方形,即长方形的长为![]() ,宽为
,宽为![]() ,此种情况有两种;第三种:
,此种情况有两种;第三种:![]() 型卡片拿掉2张,则能拼出一个正方形方形,即正方形边长为
型卡片拿掉2张,则能拼出一个正方形方形,即正方形边长为![]() .
.
(1)由图(1)和图(2)可得正方形的边长为:a+b,
由图(2)可得因式分解的等式a2+2ab+b2=(a+b)2.
故答案为a+b,a2+2ab+b2=(a+b)2;
(2)∵(2a+b)(a+2b)=2a2+5ab+2b2,
∴需要用A类卡片2张,B类卡片5张,C类卡片2张,
∴x+y+z=2+5+2=9;
故答案为9;
(3)四种拼法:理由如下:
第一种:A型卡片拿掉1张,B型卡片拿掉1张,则能拼出一个长方形,即长方形的长为5a+11b,宽为b,
∴![]()
第二种:A型卡片拿掉1张,C型卡片拿掉1张,则能拼出一个长方形,即长方形的长为3a+5b,宽为2b,
∴![]() ;
;
或者长为6a+10b,宽为b,
![]() ,此种情况共2种拼法;
,此种情况共2种拼法;
第三种:C型卡片拿掉2张,则能拼出一个正方形方形,即正方形边长为a+3b,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中
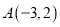 、
、 、
、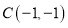 .
.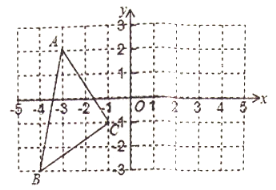
(1)在图中作出
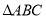 关于
关于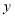 轴对称的图形
轴对称的图形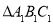 ;
;(2)写出
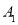 、
、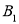 、
、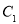 的坐标,分别是
的坐标,分别是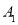 (____,_____)、
(____,_____)、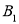 (____,_____)、
(____,_____)、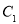 (____,_____);
(____,_____);(3)
 的面积是______________.
的面积是______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:
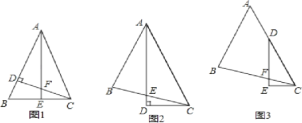
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=
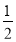 ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )
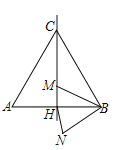
A.6B.3C.2D.1.5
相关试题

