Question

【题目】如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．在△ABC外取一点F，使FA⊥AE，FC⊥BC．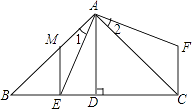

（1）求证：BE=CF；
（2）在AB上取一点M，使BM=2DE，连接ME．试判断ME与BC是否垂直，并说明理由．

Answer 1

【答案】
（1）证明：∵∠BAC=90°，AF⊥AE，

∴∠1+∠EAC=90°，∠2+∠EAC=90°

∴∠1=∠2，

又∵AB=AC，

∴∠B=∠ACB=45°，

∵FC⊥BC，

∴∠FCA=90°﹣∠ACB=90°﹣45°=45°，

∴∠B=∠FCA，

在△ABE和△ACF中，

，

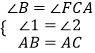∴△ABE≌△ACF（ASA），

∴BE=CF；

（2）解：如图，过点E作EH⊥AB于H，则△BEH是等腰直角三角形，

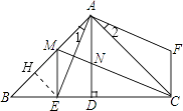
∴HE=BH，∠BEH=45°，

∵AE平分∠BAD，AD⊥BC，

∴DE=HE，

∴DE=BH=HE，

∵BM=2DE，

∴HE=HM，

∴△HEM是等腰直角三角形，

∴∠MEH=45°，

∴∠BEM=45°+45°=90°，

∴ME⊥BC．

【解析】（1）根据角的和差，求出∠1=∠2，∠B=∠FCA，根据全等三角形的判定方法ASA，得到△ABE≌△ACF，得到BE=CF；（2）根据题意得到△BEH是等腰直角三角形，由已知得到DE=BH=HE，得到△HEM是等腰直角三角形，得到ME⊥BC．