【题目】已知关于x的一元二次方程tx26x+m+4=0有两个实数根x1、x2.
(1)当m=1时,求t的取值范围;
(2)当t=1时,若x1、x2满足3| x1|=x2+4,求m的值.
参考答案:
【答案】 (1)t≤![]() 且t≠0;(2)m的值为59或
且t≠0;(2)m的值为59或![]() .
.
【解析】
(1)先将方程整理为一般形式得到![]() ,则有t≠0,根据判别式的意义可得
,则有t≠0,根据判别式的意义可得![]() ,解得
,解得![]() ,故t的取值范围为
,故t的取值范围为![]() .
.
(2)当t=1时,原式为![]() ,根据判别式的意义可以求出m的取值范围,再根据方程可以得出
,根据判别式的意义可以求出m的取值范围,再根据方程可以得出![]() ;再联系
;再联系![]() 便可求出m的取值范围.
便可求出m的取值范围.
(1)当m=1时,方程变形为tx2-6x+5=0,
根据题意得t≠0且(6)24t5≥0,
∴t≤![]() 且t≠0;
且t≠0;
(2)当t=1时,方程变形为x2-6x+m+4=0,
△=(6)24(m+4)≥0,解得m≤5,
则x1+ x2=6,x1x2=m+4,
当x1<0时,3 x1= x2+4,解得x1=5,x2=11,m+4=55,解得m=59,
当x1>0时,3 x1= x2+4,解得x1=![]() ,x2=
,x2=![]() ,m+4=
,m+4=![]() ,解得m=
,解得m=![]() ,
,
∴m的值为59或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片
 如图甲
如图甲 ,其中
,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙
如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙
如图丙 原三角形纸片ABC中,
原三角形纸片ABC中, 的大小为______
的大小为______

-
科目: 来源: 题型:
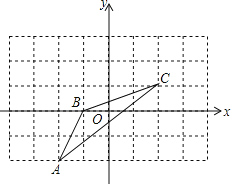
查看答案和解析>>【题目】如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.

(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(3,1),在此坐标系下,B点的坐标为 ;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为 ;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c的图象过O、B、C三点,D为此抛物线的顶点。试求出抛物线解析式及D点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=100°,AE平分∠BAC,求∠EAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)若图中一个小正方形边长为一个单位长度,请写出各点的坐标:
A1 ;B1 ;C1 ;
(3)求△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,则PF长度的最大值为 ;PF长度的最小值为 ;



第27题
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

相关试题

