Question

【题目】如图，正方形ABCD和正方形OPEF中，边AD与边OP重合，，，点M、N分别在正方形ABCD的边BC、CD上，且.将正方形OPEF以每秒2个单位的速度向右平移，当点F与点B重合时，停止平移．设平移时间为t秒.

(1)请求出t的取值范围；

(2)猜想：正方形OPEF的平移过程中，OE与NM的位置关系．并说明理由．

(3)连结DE、BE．当的面积等于7时，试求出正方形OPEF的平移时间t的值．

备用图

Answer 1

【答案】（1）；（2）OE⊥MN，证明见详解；（3）t的值为： 或.

【解析】

（1）根据题意，当AD与OP重合时，可求出AF=OF=2，BF=6，然后求出时间的最大值，即可得到t的取值范围；

（2）连接AC，BD，OE，在运动过程中有OE∥AC，由∠CNM=45°=∠CDB，得到BD∥MN，由AC⊥BD，得到AC⊥MN，即可得到OE⊥MN；

（3）由勾股定理求出BD=，由面积公式，求出△BDE的高为，连接DE，BE，连接OE与BD相交于点H，根据正方形OPEF求出OE的长度，然后得到OH的长度，由等腰三角形△OBH中，根据勾股定理求得OB的长度，然而OB=（8-2t），最后求出t的值.

（1）根据题意，当AD与OP重合时，

∴，

∴，

当点F到达点B时的时间为：（秒），

∴的取值范围是：；

（2）OE与MN是垂直的关系；

如图，连接AC，BD，OE，

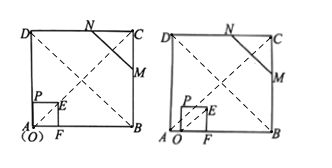
由平移性质得：OE∥AC，

由正方形性质可知，

∵∠CDB=45°=∠CNM

∴MN∥BD，

∵AC⊥BD，

∴AC⊥MN

∴OE⊥MN；

（3）连接DE，BE，连接OE与BD相交于点H，在正方形ABCD中，有AB=AD=8，

∴BD=，

由（2）知，OE⊥BD，则EH是△BDE的高，

由三角形面积公式，得：，

∴，

∴，

① 当点E在BD的下方时，如下图：

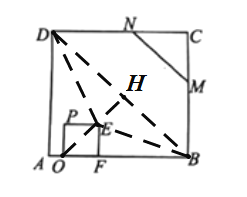
在正方形OPEF中，，

∴，

∵△OBH是等腰直角三角形，OH=BH

∵运动过程中，AO=2t，则OB=（8-2t）

由勾股定理得：，

∴，

解得：；

②当点E在BD的上方时，如图：

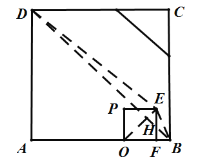
此时，，

由勾股定理得：，

解得：，

∴t的值为 或.