【题目】阅读下列材料:
1637年笛卡尔在其《几何学》中,首次应用“待定系数法”将四次方程分解为两个二次方程求解,并最早给出因式分解定理.
他认为:对于一个高于二次的关于x的多项式,“![]() 是该多项式值为0时的一个解”与“这个多项式一定可以分解为(
是该多项式值为0时的一个解”与“这个多项式一定可以分解为(![]() )与另一个整式的乘积”可互相推导成立.
)与另一个整式的乘积”可互相推导成立.
例如:分解因式![]() .
.
∵![]() 是
是![]() 的一个解,∴
的一个解,∴![]() 可以分解为
可以分解为![]() 与另一个整式的乘积.
与另一个整式的乘积.
设![]()
而![]() ,则有
,则有
 ,得
,得![]() ,从而
,从而![]()
运用材料提供的方法,解答以下问题:
(1)①运用上述方法分解因式![]() 时,猜想出
时,猜想出![]() 的一个解为_______(只填写一个即可),则
的一个解为_______(只填写一个即可),则![]() 可以分解为_______与另一个整式的乘积;
可以分解为_______与另一个整式的乘积;
②分解因式![]() ;
;
(2)若![]() 与
与![]() 都是多项式
都是多项式![]() 的因式,求
的因式,求![]() 的值.
的值.
参考答案:
【答案】(1)①:x=-1;(x+1);②![]() ;(2)3
;(2)3
【解析】
(1)①计算当x=-1时,方程成立,则![]() 必有一个因式为(x+1),即可作答;
必有一个因式为(x+1),即可作答;
②根据待定系数法原理先设另一个多项式,然后根据多项式乘多项式的计算即可求得结论;
(2))设![]() (其中M为二次整式),由材料可知,x=1,x=-2是方程
(其中M为二次整式),由材料可知,x=1,x=-2是方程![]() 的解,然后列方程组求解即可.
的解,然后列方程组求解即可.
解:(1)①![]() ,观察知,显然x=-1时,原式=0,则
,观察知,显然x=-1时,原式=0,则![]() 的一个解为x=-1;原式可分解为(x+1)与另一个整式的积.
的一个解为x=-1;原式可分解为(x+1)与另一个整式的积.
故答案为:x=-1;(x+1)
②设另一个因式为(x2+ax+b),
(x+1)(x2+ax+b)=x3+ax2+bx+x2+ax+b
=x3+(a+1)x2+(a+b)x+b
∴a+1=0,a=-1, b=3
∴多项式的另一因式为x2-x+3.
∴![]() .
.
(2)设![]() (其中M为二次整式),
(其中M为二次整式),
由材料可知,x=1,x=-2是方程![]() 的解,
的解,
∴可得 ,
,
∴②-①,得m-n=3
∴![]() 的值为3.
的值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点E是对角线
中,点E是对角线 上一点,连接
上一点,连接 .过点E作
.过点E作 交
交 的延长线于点F.若
的延长线于点F.若 ,
, ,则正方形
,则正方形 的面积为______.
的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区民用电的计费方式为:白天时段的单价为m元/度,晚间时段的单价为n元/度.某户8月份白天时段用电量比晚间时段多50%,9月份白天时段用电量比8月份白天时段用电量少60%,结果9月份的总用电量虽比8月份的总用电量多20%,但9月份的总电费却比8月份的总电费少10%,则
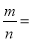 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中
中 ,E为对角线
,E为对角线 上一点,F是
上一点,F是 延长线上一点,连接
延长线上一点,连接 ,
, ,
, ,
, ,
, .
.
(1)求证:
 ;
;(2)若点G为
 的中点,连接
的中点,连接 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全关乎民生,食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存.某饮料厂为了解A、B两种饮料添加剂的添加情况,随机抽检了A种30瓶,B种70瓶,检测发现,A种每瓶比B种每瓶少1克添加剂,两种共加入了添加剂270克,求A、B两种饮料每瓶各加入添加剂多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形OPEF中,边AD与边OP重合,
 ,
, ,点M、N分别在正方形ABCD的边BC、CD上,且
,点M、N分别在正方形ABCD的边BC、CD上,且 .将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.
.将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.(1)请求出t的取值范围;
(2)猜想:正方形OPEF的平移过程中,OE与NM的位置关系.并说明理由.
(3)连结DE、BE.当
 的面积等于7时,试求出正方形OPEF的平移时间t的值.
的面积等于7时,试求出正方形OPEF的平移时间t的值.

备用图
相关试题

