【题目】如图,已知直线y=kx+2![]() 与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.
与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.

(1)求k的值;
(2)求点C的坐标;
(3)求直线CD的表达式.
参考答案:
【答案】(1) k=﹣![]() ;(2) 点C(2,0);(3) 直线CD的表达式为:y=
;(2) 点C(2,0);(3) 直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.
【解析】
(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4
,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4![]() ,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
(2)设:BC=AC=a,则OC=6﹣a,在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,即可求解;
)2+(6﹣a)2=a2,解得:a=4,即可求解;
(3)点D时AB的中点,则点D(3,![]() ),将点C、D的坐标代入一次函数表达式,即可求解.
),将点C、D的坐标代入一次函数表达式,即可求解.
解:(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,因为∠BAO=30°,所以AB=2OB=4
,因为∠BAO=30°,所以AB=2OB=4![]() ,
,
在Rt△BAO中,由勾股定理得:OA=6,把A(6,0)代入解析式y=kx+2![]() 得:k=﹣
得:k=﹣![]() ;
;
(2)设:BC=AC=a,则OC=6﹣a,
在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,
)2+(6﹣a)2=a2,解得:a=4,
则点C(2,0);
(3)点D时AB的中点,则点D(3,![]() ),
),
将点C、D的坐标代入一次函数:y=kx+b得: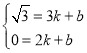 ,解得:
,解得: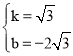 ,
,
故直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
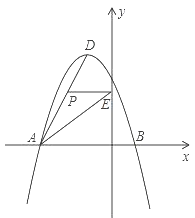
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为
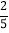 ,向左转和直行的频率均为
,向左转和直行的频率均为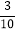 .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距d和身高h成如下所示的关系.
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
(1)直接写出身高h与指距d的函数关系式;
(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用3根火柴可拼成1个三角形,5根火柴可拼成2个三角形,7根火柴可拼成3个三角形……,按这个规律拼,用99根火柴可拼成____个三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.
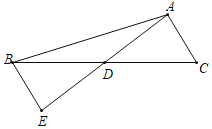
(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
相关试题

