【题目】如图，为了测量某电线杆（底部可到达）的高度，准备了如下的测量工具：

①平面镜；②皮尺；③长为2米的标杆；④高为1.5m的测角仪（测量仰角、俯角的仪器），请根据你所设计的测量方案，回答下列问题：

（1）画出你的测量方案示意图，并根据你的测量方案写出你所选用的测量工具；

（2）结合你的示意图，写出求电线杆高度的思路．

参考答案：

【答案】（1）画图见解析；（2）解法见解析.

【解析】

试题分析：（1）根据题意，设计方案如图，选用的测量工具：高为1.5m的测角仪，皮尺；

（2）根据正切函数进行设计测量方法，先测得CA的大小，因为四边形ACDE是矩形；可得DE=AC，AE=CD=1.5；根据相正切函数求得BE，即AB=BE+1.5．

试题解析：（1）测量方案示意图如图；选用的测量工具：高为1.5m的测角仪，皮尺；

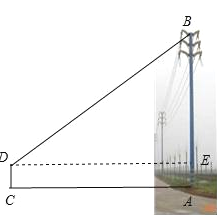
（2）CA（测角仪离电线杆的距离）=a，DC测角仪的高=1.5m，∠BDE（测角仪测的仰角）=α，

根据正切函数；可得：tanα=；

因为DE=CA=a（m），AE=CD=1.5m，

即BE=tanαa（m），

则AB=BE+AE=（tanαa+1.5）m．

故电线杆高度为（tanαa+1.5）米

关闭