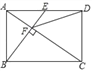
【题目】如图,E是矩形ABCD的边AD的中点,且BE⊥AC交于点F,则下列结论中正确的是( )
A. CF=3AF
B. △DCF是等边三角形
C. 图中与△AEF相似的三角形共有4个
D. tan∠CAD=![]()
参考答案:
【答案】D
【解析】分析:由![]() 又AD∥BC,所以
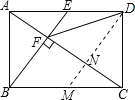
又AD∥BC,所以![]() 故A错误,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出
故A错误,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出![]() 得到CN=NF,根据线段的垂直平分线的性质可得结论,故B错误,不符合题意;根据相似三角形的判定即可求解,故C错误,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D正确,符合题意.
得到CN=NF,根据线段的垂直平分线的性质可得结论,故B错误,不符合题意;根据相似三角形的判定即可求解,故C错误,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D正确,符合题意.
详解:A.∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ∵
∵![]()
∴![]() 故A错误,不符合题意;
故A错误,不符合题意;
B. 过D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴![]()
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,
∴![]() 是等腰三角形,无法判定是等边三角形,
是等腰三角形,无法判定是等边三角形,
故B错误,不符合题意;
C. 图中与△AEF相似的三角形有△ACD,△BAF,△CBF,△CAB,△BEA共有5个,故C错误,不符合题意;
D. 设AD=a,AB=b由△BAE∽△ADC,有![]()
∵![]()
故D正确,符合题意.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
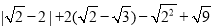 ,
,(2)解下列方程组:
i
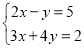 ,
,ii
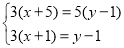 ,
,(3)求不等式的解集,并把解集在数轴上表示出来.
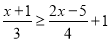 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(k﹣1)x2+2kx+2=0.
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是方程(k﹣1)x2+2kx+2=0的两个根,记
 ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两点在同一条数轴上,点A在原点的左边,到原点的距离为4,点B在原点右边,点A 到B点的距离为16.
(1)求A,B两点所表示的数:
(2)若A,B两点分别以每秒1个单位长度和3个单位长度的速度同时相向移动,在点C相遇,求点C表示的数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

-
科目: 来源: 题型:
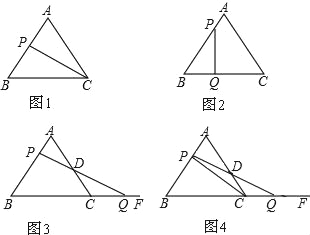
查看答案和解析>>【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t= (s)时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
(4)如图4,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
-
科目: 来源: 题型:
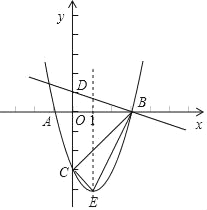
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,直线y=﹣
 x+1与y轴交于点D.
x+1与y轴交于点D.(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标;若不存在,请说明理由.
相关试题

