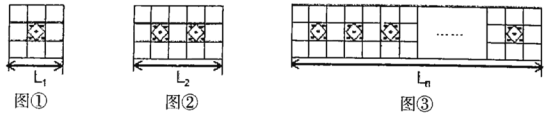
【题目】如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.
(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系;
(3)当走廊的长度L为20.5m时,请计算出所需带有花纹图案的瓷砖的块数,
参考答案:
【答案】(1)1.5,2.5;(2)L=(2n+1)×0.5;(3)需要20个有花纹的图案.
【解析】
(1)观察题目中的已知图形,可得前两个图案中有花纹的地面砖分别有:1,2个,第二个图案比第一个图案多1个有花纹的地面砖,所以可得第n个图案有花纹的地面砖有n块;第一个图案边长3×0.5=L,第二个图案边长5×0.5=L,
(2)由(1)得出则第n个图案边长为L=(2n+1)×0.5;
(3)根据(2)中的代数式,把L为20.5代入求出n的值即可.
解:(1)第一图案的长度:L1=0.5×3=1.5,第二个图案的长度:L2=0.5×5=2.5;
故答案为:1.5,2.5;
(2)观察可得:第1个图案中有花纹的地面砖有1块,第2个图案中有花纹的地面砖有2块,…故第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.5,第二个图案边长L=5×0.5,
则第n个图案边长为:L=(2n+1)×0.5;
(3)把L=20.5代入L=(2n+1)×0.5中得:
20.5=(2n+1)×0.5,
解得:n=20,
答:需要20个有花纹的图案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(1,m)、Q(n,1)在反比例函数y=
 的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.
的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.(1)求 k、b的值;
(2)O为坐标原点,C在直线y=kx+b上且AB=AC,点D在坐标平面上,顺次联结点O、B、C、D的四边形OBCD满足:BC∥OD,BO=CD,求满足条件的D点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=
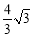 时,求∠GHE的度数.
时,求∠GHE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=
 AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8 ,其中正确的结论是______(只填序号).
,其中正确的结论是______(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程没有实数根的是( )
A. x3+2=0B. x2+2x+2=0
C.
 =x﹣1D.
=x﹣1D.  =0
=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解本校学生平均每天的课外做作业的时间情况,随机抽取部分学生进行问卷调查,并将调查的结果分为A、B、C、D四个等级(设做作业时间为t小时,A:t<1;B:1≤t<1.5;C:1.5≤t<2;D:t≥2)根据调查结果绘成了如下两幅不完整的统计图.
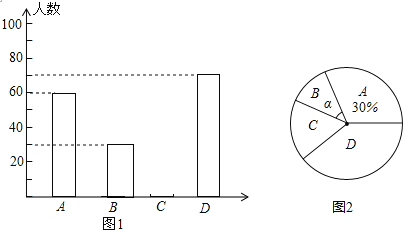
请根据图中信息,解答下列问题:
(1)本次调查中,抽取的学生人数是 ;
(2)图2中α的度数是 ,并补全图1条形统计图;
(3)该校共有2800名学生名,请估计作业时间不少于2小时的人数为 ;
(4)在此次调查中,甲班有2人平均每天的作业时间超过2小时,乙班有3名学生平均每天作业时间超过2小时,现从这5人中选取2人参加座谈会,请用树状图或列表的方法,求出“所选的2人来自不同班级”的概率.
相关试题

