【题目】如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是 . 
参考答案:
【答案】2 ![]() ﹣2
﹣2
【解析】解:如图,取AB的中点O,连接OH、OD, 
则OH=AO= ![]() AB=2,
AB=2,
在Rt△AOD中,OD= ![]() =
= ![]() =2
=2 ![]() ,
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD﹣OH=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握点和圆的三种位置关系(圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 .
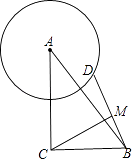
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC、DC于点E、F,连结EF.若EF=5,DF=2,则BE的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④
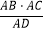 为常量.其中正确的有 .
为常量.其中正确的有 . 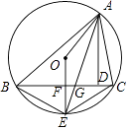
相关试题

