【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在弧AQ上且不与A点重合,但Q点可与B点重合.
(1)弧AP的长与弧QB的长之和为定值l,请直接写出l的值;
(2)请直接写出点M与AB的最大距离,此时点P,A间的距离;点M与AB的最小距离,此时半圆M的弧与AB所围成的封闭图形面积.
(3)当半圆M与AB相切时,求弧AP的长.
(注:结果保留π,cos 35°=![]() ,cos 55°=
,cos 55°=![]() )
)

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,2,
,2, ![]() ,
, ![]() ;(3)弧AP的长为
;(3)弧AP的长为![]() 或
或![]() .
.
【解析】试题分析:(1)半圆O的长度是固定不变的,由于PQ也是定值,所以![]() 的长度也是固定值,所以
的长度也是固定值,所以![]() 与
与![]() 的长之和为定值;
的长之和为定值;
(2)过点M作MC⊥AB于点C,当C与O重合时,M与AB的距离最大,此时,∠AOP=60°,AP=2;当Q与B重合时,M与AB的距离最小,此时围成的封闭图形面积可以用扇形DMB的面积减去△DMB的面积即可;
(3)当半圆M与AB相切时,此时MC=1,且分以下两种情况讨论,当C在线段OA上;当C在线段OB上,然后分别计出![]() 的长.
的长.
试题解析:
(1)如图1,连接OP、OQ,

∵AB=4,
∴OP=OQ=2,
∵PQ=2,
∴△OPQ是等边三角形,
∴∠POQ=60°,
∴![]() ,
,
又∵半圆O的长为: ![]() π×4=2π,
π×4=2π,
∴![]() =2π
=2π ![]() ,
,
∴![]() ;
;
(2)如图2,过点M作MC⊥AB于点C,连接OM,
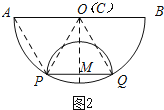
∵OP=2,PM=1,
∴由勾股定理可知:OM=![]() ,
,
当C与O重合时,
M与AB的距离最大,最大值为![]() ,
,
连接AP,
此时,OM⊥AB,
∴∠AOP=60,
∵OA=OP,
∴△AOP是等边三角形,
∴
如图3,当Q与B重合时,连接DM,
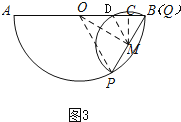
∵∠MOQ=30°,
∴MC=![]() OM=
OM=![]() ,
,
此时,M与AB的距离最小,最小值为![]() ,
,
设此时半圆M与AB交于点D,
DM=MB=1,
∵∠ABP=60°,
∴△DMB是等边三角形,
∴∠DMB=60°,
∴扇形DMB的面积为: ![]() ,
,
△DMB的面积为: ![]() MCDB=
MCDB=![]() ,
,
∴半圆M的弧与AB所围成的封闭图形面积为: ![]() ;
;
(3)当半圆M与AB相切时,
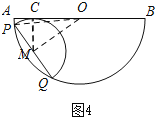
此时,MC=1,
如图4,当点C在线段OA上时,
在Rt△OCM中,
由勾股定理可求得:OC=![]() ,
,
∴cos∠AOM=![]() ,
,
∴∠AOM=35°,
∵∠POM=30°,
∴∠AOP=∠AOM∠POM=5°,
∴![]() ,
,
当点C在线段OB上时,
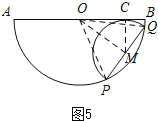
此时,∠BOM=35°,
∵∠POM=30°,
∴∠AOP=180∠POM∠BOM=115°
∴![]() ,
,
综上,弧AP的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中的三角形ABC是格点三角形,其中S=2,N=0,L=6;图中格点多边形DEFGHI所对应的S,N,L分别是 _.经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S= .(用数值作答)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式组3<x≤a的整数解恰有4个,则a的取值范围是( )
A. a>7B. 7<a<8C. 7≤a<8D. 7<a≤8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长为24,底边长y关于腰长x的函数表达式(不写出x的取值范围) 是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3a2b3)2(﹣a3b2)5÷a2b4;
(2)( )2012×(﹣1.5)2013÷(﹣1)2014;
)2012×(﹣1.5)2013÷(﹣1)2014;
(3)[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y;
(4)(5x+7y﹣3)(5x﹣7y+3);
(5)(a+2b﹣c)2;
(6)(x+2y)2(x﹣2y)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,已知AD∥BC,若要判定四边形ABCD是平行四边形,则还需要满足的条件是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
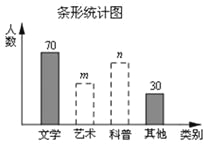
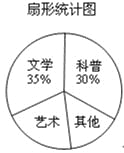
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
相关试题

