【题目】在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地,C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的图象如图所示.
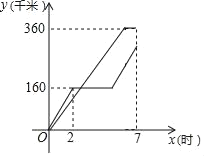
(1)在上述变化过程中,自变量是 ,因变量是 .
(2)乙车行驶的速度为 千米/小时;
(3)甲车到达B地停留了多久?B地与C地之间的距离为多少千米?
参考答案:
【答案】(1)x,y;(2)60;(3)甲车到达B地停留了3小时,B地与C地之间的距离为20千米.
【解析】
(1)根据函数定义结合函数图象得到自变量是x,因变量是y;
(2)利用已知条件知乙车比甲车早1小时即行驶6小时到达,利用路程除以时间即可得到速度;
(3)用总时间7小时减去两个2小时得到甲车停留的时间,由乙车从A行驶到C后返回得到A、C之间的路程,再减去甲车行驶的A、B之间的路程即可得到B与C之间的路程.
解:(1)由图象可得,
自变量是x,因变量是y,
故答案为:x,y;
(2)乙车行驶的速度为:360÷(7﹣1)=60千米/小时,
故答案为:60;
(3)甲车到达B地停留了:7﹣(2+2)=3(小时),
B地与C地之间的距离为:360÷2﹣160=20(千米),
答:甲车到达B地停留了3小时,B地与C地之间的距离为20千米.
-
科目: 来源: 题型:
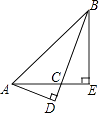
查看答案和解析>>【题目】如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:
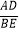 =
= 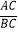 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

若某户居民
 月份用水
月份用水 ,则应收水费:
,则应收水费: 元.
元.(1)若该户居民
 月份用水
月份用水 ,则应收水费______元;
,则应收水费______元;(2)若该户居民
 、
、 月份共用水
月份共用水 (
( 月份用水量超过
月份用水量超过 月份),共交水费
月份),共交水费 元,则该户居民
元,则该户居民 ,
, 月份各用水多少立方米?
月份各用水多少立方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
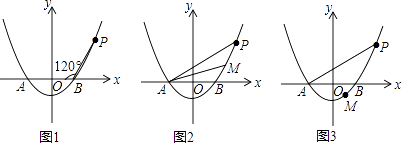
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为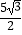 ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.

(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=APAB;④ABCP=APCB,任选一个,使ΔAPC与ΔACB相似的条件可以是( )
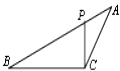
A.①或②或③
B.①或③或④
C.②或③或④
D.①或②或④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEO的度数是_____.

相关试题

