【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G. 
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
参考答案:
【答案】
(1)证明:连接OD.
∵AB与⊙O相切与点D,又AC与⊙O相切与点,
∴AC=AD,∵OC=OD,
∴OA⊥CD,
∴CD⊥OA,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC= ![]() =8,
=8,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵BD2=BFBC,
∴BF=2,
∴CF=BC﹣BF=6.OC= ![]() CF=3,
CF=3,
∴OA= ![]() =3
=3 ![]() ,
,
∵OC2=OEOA,
∴OE= ![]() ,
,
∵EM∥AC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴OM= ![]() ,EM=
,EM= ![]() ,FM=OF+OM=
,FM=OF+OM= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴CG= ![]() EM=2.
EM=2.

【解析】(1)欲证明DF∥OA,只要证明OA⊥CD,DF⊥CD即可;(2)过点作EM⊥OC于M,易知 ![]() =
= ![]() ,只要求出EM、FM、FC即可解决问题;
,只要求出EM、FM、FC即可解决问题;
【考点精析】掌握切线的性质定理是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
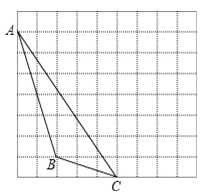
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上
(1)画出△ABC向右平移4格, 再向上平移1格后的△A1B1C1;
(2)图中BC与B1C1的关系是 ;
(3)图中△ABC的面积是
(4)请在AB上找一点D,使得线段CD平分△ABC的面积,在图上作出线段CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
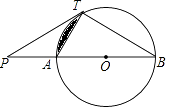
(1)求证:PT2=PAPB;
(2)若PT=TB=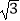 ,求图中阴影部分的面积.
,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<
 B. ﹣3<m<﹣
B. ﹣3<m<﹣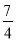 C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与坐标轴分别交于
与坐标轴分别交于 ,
, 两点,以线段
两点,以线段 为边,在第一象限内作正方形
为边,在第一象限内作正方形 ,将正方形
,将正方形 沿
沿 轴负方向,平移
轴负方向,平移 个单位长度,使点
个单位长度,使点 恰好落在直线
恰好落在直线 上,则
上,则 的值为________.
的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
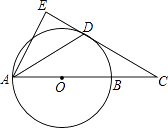
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3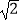 ,求弦AD的长.
,求弦AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.

(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
相关试题

