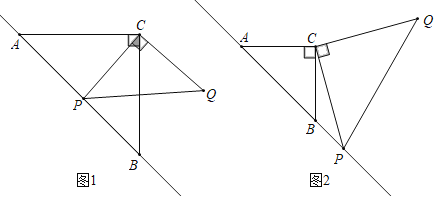
【题目】已知△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
(1)如图1,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,求线段PC的长.
,求线段PC的长.
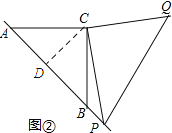
(2)如图2,若点P在AB的延长线上,猜想PA2、PB2、PC2之间的数量关系,并证明.
(3)若动点P满足![]() ,则
,则![]() 的值为 .
的值为 .
参考答案:
【答案】(1)2;(2)AP2+BP2=PQ2.理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)在等腰直角三角形ACB中,由勾股定理先求得AB的长,然后根据PA的长,可求得PB的长;过点C作CD⊥AB,垂足为D,从而可求得CD、PD的长,然后在Rt三角形CDP中依据勾股定理可求得PC的长;
(2)过点C作CD⊥AB,垂足为D,则AP=(AD+PD)=(DC+PD),PB=(DP-BD)=(PD-DC),可证明AP2+BP2=2PC2,因为在Rt△PCQ中,PQ2=2CP2,所以可得出AP2+BP2=PQ2的结论;
(3)根据点P所在的位置画出图形,然后依据题目中的比值关系求得PD的长(用含有CD的式子表示),然后在Rt△ACP和Rt△DCP中由勾股定理求得AC和PC的长度即可.
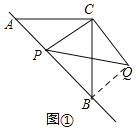
解:(1)如图①所示:
∵△ABC是等腰直直角三角形,AC=![]() ,
,
∴AB=![]() ,
,
∵PA=![]() ,
,
∴PB=AB﹣PA=![]() ,
,
∵△ABC和△PCQ均为等腰直角三角形,
∴AC=BC,PC=CQ,∠ACB=∠PCQ,
∴∠ACP=∠BCQ,
在△APC和△BQC中,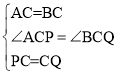 ,
,
∴△APC≌△BQC(SAS).
∴BQ=AP=![]() ,∠CBQ=∠A=45°.
,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ=![]() .
.
∴PC=![]() PQ=2.
PQ=2.
故答案为:2;
(2)AP2+BP2=PQ2.理由如下:
如图②:过点C作CD⊥AB,垂足为D.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DCPD+PD2,
PB2=(DP﹣BD)2=(PD﹣DC)2=DC2﹣2DCPD+PD2,
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2.
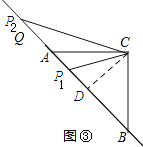
(3)如图③:过点C作CD⊥AB,垂足为D.
①当点P位于点P1处时.
![]() ,
,
![]() .
.
![]() .
.
在Rt△CP1D中,由勾股定理得: 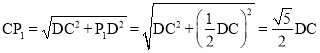 ,
,
在Rt△ACD中,由勾股定理得:![]() ,
,
![]() .
.
②当点P位于点P2处时.
![]() ,
,
∴P2A=![]() AB=DC.
AB=DC.
在Rt△CP2D中,由勾股定理得:![]() ,
,
在Rt△ACD中,由勾股定理得:![]() ,
,
![]() .
.
综上所述,![]() 的比值为
的比值为![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
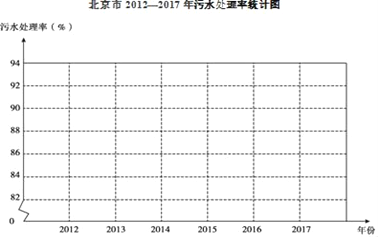
查看答案和解析>>【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份
2012
2013
2014
2015
2016
2017
污水处理率(%)
83.0
84.6
86.1
87.9
90.0
92.0
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有点
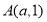 、点
、点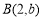 .
.(1)当A、B两点关于x轴对称时,求
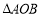 的面积;
的面积;(2)若点A向上平移2个单位,再向右平移3个单位,得到点与点B重合,求A的坐标;
(3)当线段
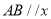 轴,且
轴,且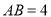 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G,AD=AE.若AD=5,DE=6,则AG的长是( )

A. 6B. 8C. 10D. 12
-
科目: 来源: 题型:
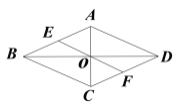
查看答案和解析>>【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
-
科目: 来源: 题型:
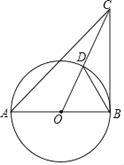
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠A=45°,以AB为直径的⊙O交CO于点D.
(1)求证:BC是⊙O的切线;
(2)连接BD,若BD=m,tan∠CBD=n,写出求直径AB的思路.
相关试题

