【题目】如图,已知⊙![]() 的半径为9cm,射线
的半径为9cm,射线![]() 经过点
经过点![]() ,OP=15 cm,射线
,OP=15 cm,射线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() .动点
.动点![]() 自P点以
自P点以![]() cm/s的速度沿射线
cm/s的速度沿射线![]() 方向运动,同时动点
方向运动,同时动点![]() 也自P点以2cm/s的速度沿射线
也自P点以2cm/s的速度沿射线![]() 方向运动,则它们从点
方向运动,则它们从点![]() 出发 s后
出发 s后![]() 所在直线与⊙
所在直线与⊙![]() 相切.
相切.
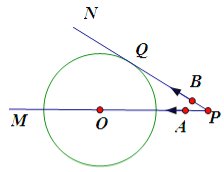
参考答案:
【答案】0.5s或10.5s.
【解析】
试题分析:PN与⊙O相切于点Q,OQ⊥PN,即∠OQP=90°,在直角△OPQ中根据勾股定理就可以求出PQ的值,过点O作OC⊥AB,垂足为C.直线AB与⊙O相切,则△PAB∽△POQ,根据相似三角形的对应边的比相等,就可以求出t的值.
试题解析: 连接OQ,
∵PN与⊙O相切于点Q,
∴OQ⊥PN,即∠OQP=90°,
∵OP=15,OQ=9,
∴PQ=![]() (cm).
(cm).
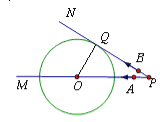
过点O作OC⊥AB,垂足为C,
∵点A的运动速度为![]() cm/s,点B的运动速度为2cm/s,运动时间为ts,
cm/s,点B的运动速度为2cm/s,运动时间为ts,
∴PA=![]() t,PB=2t,
t,PB=2t,
∵PO=15,PQ=12,
∴![]() ,
,
∵∠P=∠P,
∴△PAB∽△POQ,
∴∠PBA=∠PQO=90°,
∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ为矩形.
∴BQ=OC.
∵⊙O的半径为,
∴BQ=OC=9时,直线AB与⊙O相切.
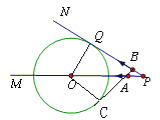
①当AB运动到如图1所示的位置,
BQ=PQ-PB=12-2t,
∵BQ=9,
∴8-4t=9,
∴t=0.25(s).
②当AB运动到如图2所示的位置,
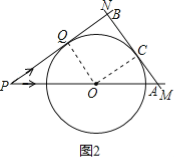
BQ=PB-PQ=2t-12,
∵BQ=9,
∴2t-12=9,
∴t=10.5(s).
∴当t为0.5s或10.5s时直线AB与⊙O相切.
考点: 1.切线的判定;2.勾股定理;3.矩形的性质;4.相似三角形的判定与性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图
 ,在平面直角坐标系
,在平面直角坐标系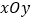 中,直线
中,直线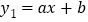 与双曲线
与双曲线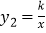 交于
交于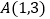 和
和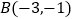 两点.
两点.观察图象可知:①当
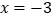 或
或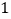 时,
时,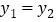 ;②当
;②当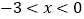 或
或 时,
时,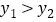 ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式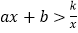 的解集.
的解集.有这样一个问题:求不等式
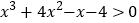 的解集.
的解集.某同学根据学习以上知识的经验,对求不等式
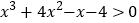 的解集进行了探究.
的解集进行了探究.下面是他的探究过程,请将(
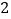 )、(
)、(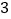 )、(
)、(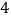 )补充完整:
)补充完整:(
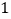 )将不等式按条件进行转化:
)将不等式按条件进行转化:当
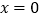 时,原不等式不成立.
时,原不等式不成立.当
 时,原不等式可以转化为
时,原不等式可以转化为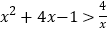 .
.当
 时,原不等式可以转化为
时,原不等式可以转化为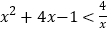 .
.(
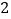 )构造函数,画出图象.
)构造函数,画出图象.设
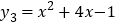 ,
,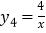 ,在同一坐标系中分别画出这两个函数的图象.
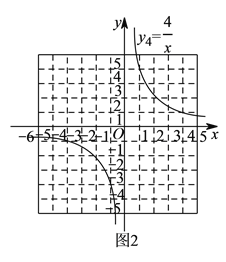
,在同一坐标系中分别画出这两个函数的图象.双曲线
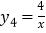 如图
如图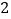 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线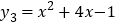 .(不用列表)
.(不用列表)(
 )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足
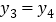 的所有
的所有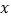 的值为__________.
的值为__________.(
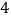 )借助图象,写出解集.
)借助图象,写出解集.结合(
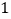 )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式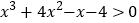 的解集为__________.
的解集为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图,在△
 中,把
中,把 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,把
,把 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 ,连接
,连接 ,当
,当 时,我们称△
时,我们称△ 是△
是△ 的“旋补三角形”,△
的“旋补三角形”,△ 边
边 上的中线
上的中线 叫做
叫做 的“旋补中线”,点
的“旋补中线”,点 叫做“旋补中心”.
叫做“旋补中心”.⑴ 特例感知:在如图、如图中,
 是
是 的“旋补三角形”,
的“旋补三角形”, 是
是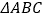 的“旋补中线”.
的“旋补中线”.① 如图,当
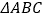 为等边三角形时,
为等边三角形时, 与
与 的数量关系为
的数量关系为 =
=  ;
;② 如图,当
 ,
, 时,则
时,则 长为 .
长为 .⑵ 精确作图:如图,已知在四边形
 内部存在点
内部存在点 ,使得
,使得 是
是 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点 (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)⑶ 猜想论证:在如图中,当△
 为任意三角形时,猜想
为任意三角形时,猜想 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
 =________%,
=________%,  =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC
 轴,直线CB
轴,直线CB 轴:
轴:(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

相关试题

