【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

参考答案:
【答案】(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
【解析】
(1)根据题意得出A和C的横坐标相同,B和C的纵坐标相同,得出A(5,3),C(5,6),由角平分线的性质得出B的坐标;
(2)求出BC=5-(-6)=11,即可得出△ABC的面积;
(3)设P的坐标为(a,-a),则△BCP的面积=![]() ×11×(6+a),根据题意得出不等式12<
×11×(6+a),根据题意得出不等式12<![]() ×11×(6+a)<16,解不等式即可.
×11×(6+a)<16,解不等式即可.
解:(1)如图所示:
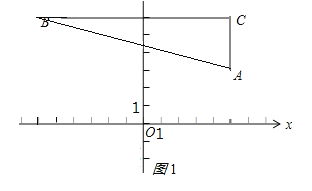
∵AC⊥x轴,CB⊥y轴,
∴A和C的横坐标相同,B和C的纵坐标相同,
∴A(5,3),C(5,6),
∵点B的纵坐标为6且横纵坐标互为相反数,
∴B(-6,6);
(2)∵BC=5-(-6)=11,
∴△ABC的面积=![]() ×11×(6-3)=
×11×(6-3)=![]() ;
;
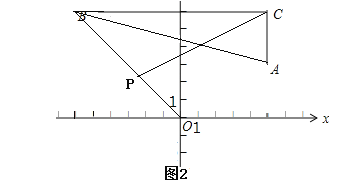
(3)设P的坐标为(a,-a),
则△BCP的面积=![]() ×11×(6+a),
×11×(6+a),
∵△BCP面积大于12小于16,
∴12<![]() ×11×(6+a)<16,
×11×(6+a)<16,
解得:-![]() <a<-
<a<-![]() ;
;
即点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
故答案为:(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙
 的半径为9cm,射线
的半径为9cm,射线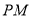 经过点
经过点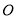 ,OP=15 cm,射线
,OP=15 cm,射线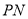 与⊙
与⊙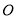 相切于点
相切于点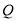 .动点
.动点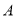 自P点以
自P点以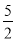 cm/s的速度沿射线
cm/s的速度沿射线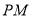 方向运动,同时动点
方向运动,同时动点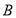 也自P点以2cm/s的速度沿射线
也自P点以2cm/s的速度沿射线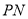 方向运动,则它们从点
方向运动,则它们从点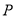 出发 s后
出发 s后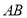 所在直线与⊙
所在直线与⊙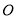 相切.
相切.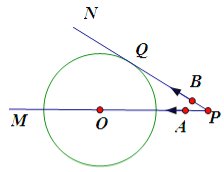
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,
 =
= 时,求DE的长.
时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,则多了3钱,每人出7钱,则少4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为________________.

相关试题

