【题目】如图,抛物线y=ax2+bx+c的顶点为M（﹣2,﹣4），与x轴交于A、B两点,且A（﹣6,0），与y轴交于点C．

（1）求抛物线的函数解析式；
（2）求△ABC的面积；
（3）能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大？若能,请求出点P的坐标；若不能，请说明理由．

参考答案：

【答案】
（1）解：设此函数的解析式为y=a（x+h）2+k，
∵函数图象顶点为M（﹣2，﹣4），
∴y=a（x+2）2﹣4，
又∵函数图象经过点A（﹣6，0），
∴0=a（﹣6+2）2﹣4解得a= ，
∴此函数的解析式为y= （x+2）2﹣4，
即y= x2+x﹣3
（2）解：∵点C是函数y= x2+x﹣3的图象与y轴的交点，
∴点C的坐标是（0，﹣3），
又当y=0时，有y= x2+x﹣3=0，
解得x1=﹣6，x2=2，
∴点B的坐标是（2，0），
则S△ABC= |AB||OC|= ×8×3=12
（3）解：假设存在这样的点，过点P作PE⊥x轴于点E，交AC于点F．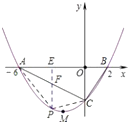

设E（x，0），则P（x， x2+x﹣3），
设直线AC的解析式为y=kx+b，
∵直线AC过点A（﹣6，0），C（0，﹣3），
∴ ，解得 ，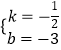
∴直线AC的解析式为y=﹣ x﹣3，
∴点F的坐标为F（x，﹣ x﹣3），
则|PF|=﹣ x﹣3﹣（ x2+x﹣3）=﹣ x2﹣ x，
∴S△APC=S△APF+S△CPF= |PF||AE|+ |PF||OE|
= |PF||OA|= （﹣ x2﹣ x）×6=﹣ x2﹣ x=﹣ （x+3）2+ ，
∴当x=﹣3时，S△APC有最大值 ，此时点P的坐标是P（﹣3，﹣ ）
【解析】根据顶点坐标公式即可求得a、b、c的值，即可解题；
易求得点B、C的坐标，即可求得OC的长，即可求得△ABC的面积，即可解题；
作PE⊥x轴于点E，交AC于点F，可将△APC的面积转化为△AFP和△CFP的面积之和，而这两个三角形有共同的底PF，这一个底上的高的和又恰好是A、C两点间的距离，因此若设设E（x，0），则可用x来表示△APC的面积，得到关于x的一个二次函数，求得该二次函数最大值，即可解题．

关闭