【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1 , x2 , x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( ) 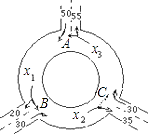
A.x1>x2>x3
B.x1>x3>x2
C.x2>x3>x1
D.x3>x2>x1
参考答案:
【答案】C
【解析】解:依题意,有x1=50+x3﹣55=x3﹣5=>x1<x3 ,
同理,x2=30+x1﹣20=x1+10=>x1<x2 ,
同理,x3=30+x2﹣35=x2﹣5=>x3<x2 .
故选C.
【考点精析】本题主要考查了整式加减法则的相关知识点,需要掌握整式的运算法则:(1)去括号;(2)合并同类项才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为( ).(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)

A.164m B.178m C.200m D.1618m
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出旋转后的点关于原点的对称点,这称为一次变换,已知点A的坐标为(﹣1,0),则点A经过连续2016次这样的变换得到的点
 的坐标是 .
的坐标是 . -
科目: 来源: 题型:
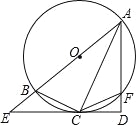
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
(1)求证:CD是⊙O的切线;
(2)若AD=6,DE=8,求BE的长;
(3)求证:AF+2DF=AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中直线y=-2x+12与x轴交于点A,与y轴交于点B,
与直线y=x交于点C.
(1)求点C的坐标
(2)求三角形OAC的面积.

相关试题

