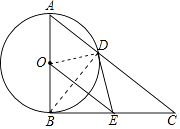
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE. 
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD= ![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
参考答案:
【答案】
(1)解:连接BD、OD,如图,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E∵为斜边BC的中点,
∴CE=DE=BE= ![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线
(2)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴BC:CD=AC:BC,
即BC2=ACCD.
∴BC2=2CDOE
(3)解:∵OE∥AC,
∴∠BOE=∠BAD,
在Rt△OBE中,cos∠BOE= ![]() =
= ![]() ,
,
设OB=3t,OE=5t,
则BE=4t,
∴4t=6,解得t= ![]() ,
,
∴OE=5t= ![]()
【解析】(1)利用圆周角定理得到∠ADB=90°,再利用直角三角形斜边上的中线性质得CE=DE=BE= ![]() BC,则∠C=∠CDE,加上∠A=∠ADO得到∠C+∠A=90°,然后证明∠ODE=90°,从而根据切线的判定方法可判定DE为⊙O的切线;(2)先证明OE是△ABC的中位线得到AC=2OE,再证明△ABC∽△BDC,则利用相似比和比例的性质可得到结论;(3)利用OE∥AC得到∠BOE=∠BAD,根据余弦定义得到cos∠BOE=
BC,则∠C=∠CDE,加上∠A=∠ADO得到∠C+∠A=90°,然后证明∠ODE=90°,从而根据切线的判定方法可判定DE为⊙O的切线;(2)先证明OE是△ABC的中位线得到AC=2OE,再证明△ABC∽△BDC,则利用相似比和比例的性质可得到结论;(3)利用OE∥AC得到∠BOE=∠BAD,根据余弦定义得到cos∠BOE= ![]() =
= ![]() ,则可设OB=3t,OE=5t,利用勾股定理得到BE=4t,于是得到4t=6,然后求出t后计算5t即可.
,则可设OB=3t,OE=5t,利用勾股定理得到BE=4t,于是得到4t=6,然后求出t后计算5t即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )

A. 极差是40 B. 中位数是58 C. 平均数大于58 D. 众数是5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某班参加课外活动的总共有30人,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2,那么参加“其它”活动的人数有________人.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF,∠FDC=30°,求∠BEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
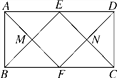
A. 正方形 B. 菱形 C. 矩形 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)被抽样调查的学生有 ________人,并补全条形统计图;
(2)每天户外活动时间的中位数是________ (小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有________人?

相关试题

