【题目】在平面直角坐标系第一象限中,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度匀速向点
个单位长度的速度匀速向点![]() 方向运动,与此同时,
方向运动,与此同时,![]() 轴上动点
轴上动点![]() 从点
从点![]() 出发,以相同的速度向右运动, 两动点运动时间为:
出发,以相同的速度向右运动, 两动点运动时间为:![]() , 以
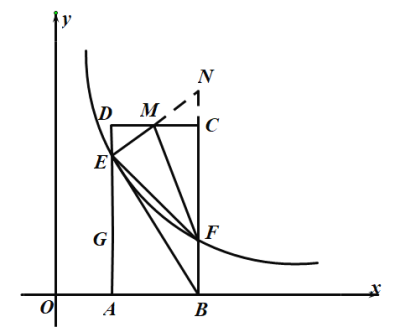
, 以![]() 分别为边作矩形
分别为边作矩形![]() , 过点
, 过点![]() 作双曲线交线段
作双曲线交线段![]() 于点
于点![]() ,作
,作![]() 中点
中点![]() ,连接
,连接![]()
(1)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(2)若![]() 平分
平分![]() , 则
, 则![]() 的值为多少?
的值为多少?
(3)若![]() 为直角, 则
为直角, 则![]() 的值为多少?
的值为多少?

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 时,E点的坐标,然后求出双曲线的解析式,进而可求出F点的坐标;
时,E点的坐标,然后求出双曲线的解析式,进而可求出F点的坐标;
(2)先求出E点的坐标,然后求出双曲线的解析式,进而可求出F点的坐标,然后利用角平分线的定义和平行线的性质得出![]() ,即可求出t的值;
,即可求出t的值;
(3)延长EM,BC交于点N,先求出E点的坐标,然后求出双曲线的解析式,进而可求出F点的坐标,然后通过平行线的性质和中点得出![]() ,则有
,则有![]() ,进而得出
,进而得出![]() ,然后再证明
,然后再证明![]() ,得出
,得出![]() ,从而建立一个关于t的方程,解方程求解即可.
,从而建立一个关于t的方程,解方程求解即可.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设双曲线的解析式为![]() ,
,
将点E代入解析式中,有![]() ,
,
∴双曲线的解析式为![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() .
.
设双曲线的解析式为![]() ,
,
将点E代入解析式中,有![]() ,
,
∴双曲线的解析式为![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() .
.
∵BE平分![]() ,
,
![]() .
.
∵四边形ABCD为矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)延长EM,BC交于点N,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴![]() .
.
设双曲线的解析式为![]() ,
,
将点E代入解析式中,有![]() ,
,
∴双曲线的解析式为![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵点M为CD中点,
∴![]() .
.
在![]() 和
和![]() 中,
中,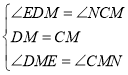
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() 为直角,
为直角,
![]() ,
,
在![]() 和
和![]() 中,
中,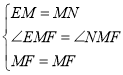
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
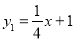 与
与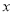 轴交于点
轴交于点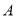 ,与
,与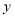 轴交于点
轴交于点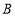 ,与反比例函
,与反比例函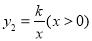 的图象交于点
的图象交于点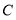 ,且
,且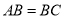 .
.(1)求点
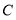 的坐标和反比例函数
的坐标和反比例函数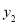 的解析式;
的解析式;(2)点
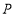 在
在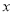 轴上,反比例函数
轴上,反比例函数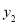 图象上存在点
图象上存在点 ,使得四边形
,使得四边形 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.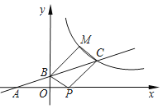
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B、∠D的两边分别平行。

(1)在图①中,∠B与∠D的数量关系为相等相等。
(2)在图②中,∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
试分别说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有( )

A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数
20
50
100
200
500
参加“半程马拉松”人数
15
33
72
139
356
参加“半程马拉松”频率
0.750
0.660
0.720
0.695
0.712
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
相关试题

