【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)欲证明AD=CE,只要证明△ABD≌△CBE即可;
(2)如图2中,倍长BE到H,连CH,DH.首先证明△DBH是等边三角形,由(1)可知,△ABD≌△CBH,推出AD=CH,∠A=∠HCB=∠ABC=60°,推出BF∥CH,推出∠F=∠ECH,再证明△EBF≌△EHC,推出BF=CH,由此即可证明.
(1)证明:如图1中,
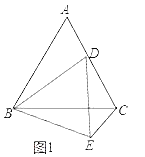
∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
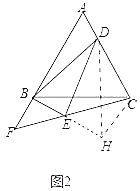
在△ABD和△CBE中, 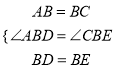 ,
,
∴△ABD≌△CBE,
∴AD=CE.
(2)如图2中,倍长BE到H,连CH,DH.
∵BE=EH,DE⊥BH,
∴DB=DH,∠BDE=∠HDE=30°,
∴∠BDH=60°,
∴△DBH是等边三角形,
由(1)可知,△ABD≌△CBH,
∴AD=CH,∠A=∠HCB=∠ABC=60°,
∴BF∥CH,
∴∠F=∠ECH,
在△EBF和△EHC中, 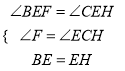 ,
,
∴△EBF≌△EHC,
∴BF=CH,
∴AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
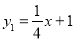 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点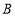 ,与反比例函
,与反比例函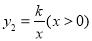 的图象交于点
的图象交于点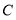 ,且
,且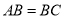 .
.(1)求点
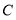 的坐标和反比例函数
的坐标和反比例函数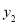 的解析式;
的解析式;(2)点
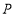 在
在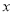 轴上,反比例函数
轴上,反比例函数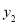 图象上存在点
图象上存在点 ,使得四边形
,使得四边形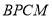 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.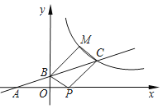
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系第一象限中,已知点
 坐标为
坐标为 ,点
,点 坐标为
坐标为 ,点
,点 坐标为
坐标为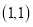 ,动点
,动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度匀速向点
个单位长度的速度匀速向点 方向运动,与此同时,
方向运动,与此同时, 轴上动点
轴上动点 从点
从点 出发,以相同的速度向右运动, 两动点运动时间为:
出发,以相同的速度向右运动, 两动点运动时间为: , 以
, 以 分别为边作矩形
分别为边作矩形 , 过点
, 过点 作双曲线交线段
作双曲线交线段 于点
于点 ,作
,作 中点
中点 ,连接
,连接
(1)当
 时,求点
时,求点 的坐标.
的坐标.(2)若
 平分
平分 , 则
, 则 的值为多少?
的值为多少?(3)若
 为直角, 则
为直角, 则 的值为多少?
的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B、∠D的两边分别平行。

(1)在图①中,∠B与∠D的数量关系为相等相等。
(2)在图②中,∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
试分别说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有( )

A. 1B. 2C. 3D. 4
相关试题

