搜索
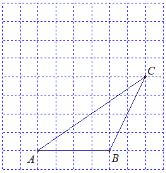
【题目】如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．
（1）画出△ABC向左平移2个单位,再向上平移3个单位后得到的△A1B1C1；
（2）图中AC与A1C1的关系是： ；
（3）画出△ABC中BC边上的中线AD；
（4）△ACD的面积为 ．
参考答案：
【答案】（1）见解析；（2）平行且相等；（3）见解析；（4）4
【解析】
(1)根据网格结构找出点A、B、C向左平移2个单位,再向上平移3个单位后的对应点A1、B1、C1的位置，然后顺次连接即可；（2）根据平移的性质解答；（3）根据网格结构确定出BC的中点D，然后连接AD即可；（4）利用△ACD所在的矩形的面积减去四周两个直角三角形的面积，列式计算即可得解．
解(1) 图中△A1B1C1即为所求;
(2) AC与A1C1的关系是：平行且相等；
(3)图中AD即为所求;
(4)S △ACD=4×6-
×4×6-×4×4=24-12-8=4.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解决问题：
一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5千米到达小颖家，然后向西走了10千米到达小明家，最后回到超市．
（1）以超市为原点，以向东的方向为正方向，用1个单位长度表示1千米，在数轴上表示出小明家，小彬家，小颖家的位置．
（2）小明家距小彬家多远？
（3）货车一共行驶了多少千米？
（4）货车每千米耗油0.2升，这次共耗油多少升？
-
科目： 来源： 题型：
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示4和1的两点之间的距离为|4﹣1|= ；表示5和﹣2两点之间的距离为|5﹣（﹣2）|=|5+2|= ；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|，如果表示数a和﹣2的两点之间的距离是3，那么a= ．
（2）若数轴上表示数a的点位于﹣4与2之间，求|a+4|+|a﹣2|的值；
（3）当a= 时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，AF、CE分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是__________．（只需写出一个即可，图中不能再添加别的“点”和“线”）
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了更好治理西太湖水质，保护环境，市治污公司决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格，月处理污水量如下表：
经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买4台B型设备少4万元．
（1）求a、b的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过47万元，你认为该公司有哪几种购买方案；
（3）在（2）问的条件下，若该月要求处理西太湖的污水量不低于1860吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读短文，然后回答短文后面所给出的问题：
对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定M{a，b，c}表示a，b，c这三个数的平均数，min{a，b，c}表示a，b，c这三个数中最小的数，max{a，b，c}表示a，b，c这三个数中最大的数．例如：M{﹣1，2，3}＝
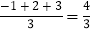，min{﹣1，2，3}＝﹣1，max{﹣1，2，3}＝3；M{﹣1，2，a}＝
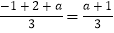，min{﹣1，2，a}＝
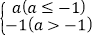．（1）请填空：max{c﹣1，c，c＋1}＝ ；若m＜0，n＞0，min{3m，（n＋3）m，﹣mn}＝ ；
（2）若min{2，2x＋2，4﹣2x}＝2，求x的取值范围；
（3）若M{2，x＋1，2x}＝min{2，x＋1，2x}，求x的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：
如图①，在△ABC中，点D、E、F分别在边AB、AC、CB上，且DE∥BC，EF∥AB，若∠ABC＝65°，求∠DEF的度数．请将下面的解答过程补充完整，并填空(理由或数学式)：
解：∵DE∥BC( )
∴∠DEF＝ ( )
∵EF∥AB
∴ ＝∠ABC( )
∴∠DEF＝∠ABC( )
∵∠ABC＝65°
∴∠DEF＝
应用：
如图②，在△ABC中，点D、E、F分别在边AB、AC、BC的延长线上，且DE∥BC，EF∥AB，若∠ABC＝β，则∠DEF的大小为 (用含β的代数式表示)．
相关试题
