【题目】为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.
(1)按图示规律,第一图案的长度L1=m;第二个图案的长度L2=m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数及瓷砖总数.
参考答案:
【答案】
(1)1.8,3
(2)解:观察图形可得:
第1个图案中有花纹的地面砖有1块,
第2个图案中有花纹的地面砖有2块,
…
则第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.6,第二个图案边长L=5×0.6,则第n个图案边长为L=(2n+1)×0.6
(3)解:把L=36.6代入L=(2n+1)×0.6中得:
36.6=(2n+1)×0.6,
解得:n=30,
瓷砖总数=9+6×29=183
答:需带有花纹图案的瓷砖的块数是30.瓷砖总数为183块
【解析】先观察图形得:第1个图案中有花纹的地面砖有1块,第2个图案中有花纹的地面砖有2块,…则第n个图案中有花纹的地面砖有n块;则第n个图案边长为L=(2n+1)×0.6。再得出结论,最后进行求解
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中,点A、B、C都在第一象限内,现将△ABC的三个顶点的横坐标保持不变,纵坐标都乘-1,得到一个新的三角形,则( )。
A. 新三角形与△ABC关于x轴对称 B. 新三角形与△ABC关于y轴对称
C. 新三角形的三个顶点都在第三象限内 D. 新三角形是由△ABC沿y轴向下平移一个单位长度得到的
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x﹣(x+10)=6x
(2)1﹣ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= .
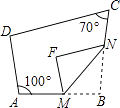
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
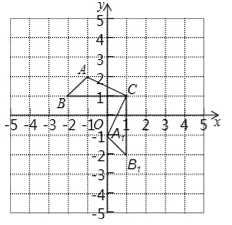
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个内角是50°,则这个等腰三角形的底角的大小是( )
A. 65°或80° B. 80°或40° C. 65°或50° D. 50°或80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:32°24′_____32.5°.(填“<”或“>”)
相关试题

