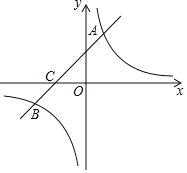
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
参考答案:
【答案】⑴![]() ,
,![]() ;⑵
;⑵![]() 的最大值为
的最大值为![]() ,
,![]() ;⑶
;⑶![]() 或
或![]() .
.
【解析】
(1)利用待定系数法,即可得到反比例函数和一次函数的解析式;
(2)根据一次函数y1=x+2,求得与y轴的交点P,此交点即为所求;
(3)根据AB两点的横坐标及直线与双曲线的位置关系求x的取值范围.
⑴.∵![]() 在反比例函数
在反比例函数![]() 上
上
∴![]()
∴反比例函数的解析式为![]()
把![]() 代入
代入![]() 可求得
可求得![]()
∴![]() .
.
把![]() 代入
代入![]() 为
为![]() 解得
解得![]() .
.
∴一次函数的解析式为![]() .
.
⑵![]() 的最大值就是直线
的最大值就是直线![]() 与两坐标轴交点间的距离.
与两坐标轴交点间的距离.
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
令![]() ,则
,则![]() ,解得
,解得![]() ,∴
,∴![]()
令![]() ,则
,则![]() ,,∴
,,∴![]()
∴![]() ,
,![]()
∴![]() 的最大值为
的最大值为![]() .
.
⑶根据图象的位置和图象交点的坐标可知:
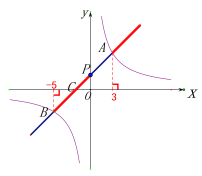
当![]() 时
时![]() 的取值范围为;
的取值范围为;![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是_____;
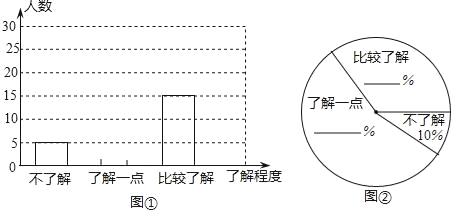
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
(3)请你估计该校八年级约有多少名学生比较了解“低碳”知识.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1与∠2互补,
 .
.那么
 .
.
证明如下:
 (已知)
(已知) _________(_____________________________________________)
_________(_____________________________________________)∴
 (__________________________________)
(__________________________________)∵
 (已知)
(已知)∴
 (等量代换)
(等量代换)∴____________∥___________(__________________________________)
∴
 (__________________________________)
(__________________________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是( ).
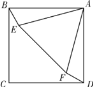
A.15°B.165°C.15°或165°D.90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
相关试题

