【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P,B,C为顶点的三角形是等腰三角形,则P,D(P,D两点不重合)两点间的最短距离为 . 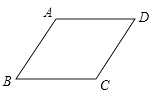
参考答案:
【答案】2 ![]() ﹣2
﹣2
【解析】解:①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点P与点A重合时,PD值最小,为2;
②若以边PC为底,∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD最小,最小值为2√3﹣2;
③若以边PB为底,∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;
综上所述,PD的最小值为2 ![]() ﹣2.
﹣2.
根据等腰三角形的性质,①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,由直线外一点与直线上所有点连线的线段中垂线段最短,得到当点P与点A重合时,PD值最小;②若以边PC为底,∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD最小;③若以边PB为底,∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;得出PD的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形
 ,过
,过 做
做 于点
于点 ,
, ,若在平行四边形内取一点,则该点到平行四边形的四个顶点的距离均不小于1的概率为_______.
,若在平行四边形内取一点,则该点到平行四边形的四个顶点的距离均不小于1的概率为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2020年83岁的钟南山奋战在抗击疫情的最前线,成为全国人民最敬佩的硬核男神,他有强健的身体,这都是得益于几十年如一日的坚持锻炼.在本次疫情中打败新冠肺炎还需要自身免疫力,同学们都应该加强身体锻炼,为了了解同学们在线上教学中体育锻炼的情况,在返校后某初中对600名初一学生进行了体育测试,其中对仰卧起坐成绩进行了整理,绘制成如下不完整的统计图:

根据统计图,回答下列问题.
(1)请将条形统计图补充完整;
(2)扇形统计图中,
 =_____,得8分所对应扇形的圆心角度数为_____;
=_____,得8分所对应扇形的圆心角度数为_____;(3)若本校共有3000名初一学生,请估算体育测试成绩为10分的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图1,AC和BD相交于点O,OA=OC,OB=OD,求证:DC∥AB.
(2)如图2,在⊙O中,直径AB=6,AB与弦CD相交于点E,连接AC、BD,若AC=2,求cosD的值.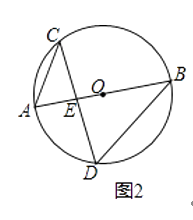
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计),第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车,小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林,离入口处的路程
 (米)与时间
(米)与时间 (分)的函数关系如图2所示.
(分)的函数关系如图2所示.(1)求第一班车从入口处到达塔林的时间.
(2)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变).
(3)若小聪在8:30至8:50之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过3分钟的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:①若
 则
则 ②若
②若 则
则 ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A. 1B. 2C. 3D. 4
相关试题

