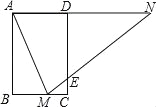
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)当M为BC中点时,求ME的长.
参考答案:
【答案】(1)证明详见解析;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】
试题分析:(1)根据矩形的性质和平行线的性质证明即可;
(2)作NH⊥AM于H,证明△NAH∽△AMB,根据相似三角形的性质得到ANBM=![]() ,根据勾股定理计算即可;
,根据勾股定理计算即可;
(3)由(2)的结论,结合相似三角形的性质求出CE,根据勾股定理计算即可.
试题解析:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
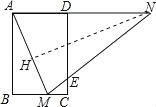
(2)如图,作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=![]() AM,
AM,
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴![]() ,
,
∴ANBM=AHAM=![]() ,
,
在Rt△AMB中,![]() ,
,
∵BM≤2,
∴9+![]() ≤13,
≤13,
∴ANBM≤![]() ,
,
即当BM=2时,BMAN的最大值为![]() ;
;
(3)解:∵M为BC中点,
∴BM=CM=![]() BC=1,
BC=1,
由(2)得,ANBM=![]() ,
,
∵![]() =
=![]() =10,
=10,
∴AN=5,
∴DN=5﹣2=3,
设DE=x,则CE=3﹣x,
∵AN∥BC,
∴![]() ,即
,即![]() ,
,
解得,x=![]() ,即CE=
,即CE=![]() ,
,
∴CE=![]() ,
,
∴ME=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子变形正确的是( )
A. ﹣(m+2)=﹣m+2 B. 3m﹣6m=﹣3m C. 2(a+b)=2a+b D. π﹣3=3﹣π
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+kx-3=0有一个根为1,则k的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湛江市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000B.5500(1﹣x)2=4000C.4000(1﹣x)2=5500D.4000(1+x)2=5500
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
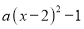 过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
过点C(4,3),交x轴于A,B两点(点A在点B的左侧).(1)求抛物线的解析式,并写出顶点M的坐标;
(2)连接OC,CM,求tan∠OCM的值;
(3)若点P在抛物线的对称轴上,连接BP,CP,BM,当∠CPB=∠PMB时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)2n﹣(2﹣n)+(6n﹣2),其中n=﹣2;
(2)﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)],其中a=﹣2,b= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O1和⊙O2的半径是2 cm和3 cm,两圆的圆心距4 cm,则两圆的位置关系是( )
A.内切B.相交C.外切D.外离
相关试题

