【题目】如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( ) 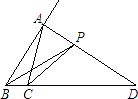
A.m+n>b+c
B.m+n<b+c
C.m+n=b+c
D.无法确定
参考答案:
【答案】A
【解析】解:在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠A的外角平分线,
∴∠CAD=∠EAD,
在△ACP和△AEP中, 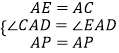 ,
,
∴△ACP≌△AEP(SAS),
∴PE=PC,
在△PBE中,PB+PE>AB+AE,
∵PB=m,PC=n,AB=c,AC=b,
∴m+n>b+c.
故选A.
在BA的延长线上取点E,使AE=AC,连接EP,证明△ACP和△AEP全等,推出PE=PC,根据三角形任意两边之和大于第三边即可得到m+n>b+c.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,错误的是( )
A. 平行四边形的对角线互相平分
B. 菱形的对角线互相垂直平分
C. 矩形的对角线相等且互相垂直平分
D. 角平分线上的点到角两边的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:3x=x(x+5)﹣8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
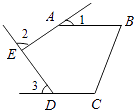
查看答案和解析>>【题目】如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=kx-1向上平移2个单位长度,可得直线的解析式为( )
A. y=kx+1 B. y=kx-3 C. y=kx+3 D. y=kx-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正六边形外接圆的半径为4,则它的边长为_____.
相关试题

