【题目】如图,在直角坐标系中,正方形OABC的顶点B的坐标为(3,3),直线CD交直线OA于点D,直线OE交线段AB于E,且CD⊥OE,垂直为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为________.
,则△OFC的周长为________.

参考答案:
【答案】![]()
【解析】
先证明ΔCOD≌ΔOAE,推出ΔOCF的面积=四边形DAEF的面积,设OF=x,FC=y,由勾股定理和面积公式得出xy和![]() 的值,利用
的值,利用![]() 求出x+y值,即可得到周长.
求出x+y值,即可得到周长.
∵正方形OABC的顶点B的坐标为(3,3),
∴OC=OA=3,∠OAB=90,且正方形的面积为9,
∵阴影部分的面积是正方形OABC的面积的![]() ,
,
∴阴影的面积为9×![]() =3,
=3,
∵CD⊥OE,
∴∠AOE+∠ODC=90,
又∵∠OCD+∠ODC=90,
∴∠OCD=∠AOE,
在ΔCOD和ΔOAE中
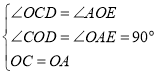
∴ΔCOD≌ΔOAE(AAS),
∴ΔOCF的面积=四边形DAEF的面积=3÷2=![]() ,
,
设设OF=x,FC=y,
则xy=3,![]() ,
,
∴![]() ,
,
∴![]() ,
,
所以△OFC的周长为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
 ,
, ,
, ,且
,且 、
、 、
、 三点在一直线上,请填写
三点在一直线上,请填写 的理由.
的理由.
解:在
 与
与 中,
中, (已知),
(已知), (已知),
(已知), (已知),
(已知),所以

所以

 ________(________)
________(________)所以
 (等式性质),
(等式性质),即
 ________
________ ________.
________.因为
 (________)
(________)即
 ,
,所以
 (________).
(________).所以
 (等量代换).
(等量代换). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.
 B.
B.
C.
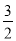 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 (1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的
 ;
;(2)如图 (2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,小东妈妈准备购买若干个粽子和咸鸭蛋(每个棕子的价格相同,每个咸鸭蛋的价格相同).已知某超市粽子的价格比咸鸭蛋的价格贵1.8元,小东妈妈发现,花30元购买粽子的个数与花12元购买的咸鸭蛋个数相同.
(1)求该超市粽子与咸鸭蛋的价格各是多少元?
(2)小东妈妈计划购买粽子与咸鸭蛋共18个,她的一张购物卡上还有余额40元,若只用这张购物卡,她最多能购买粽子多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC 中,AB、AC 边的垂直平分线相交于点 O,分别交 BC 边于点 M、N,连接 AM,AN.

(1)若△AMN 的周长为 6,求 BC 的长;
(2)若∠MON=30°,求∠MAN 的度数;
(3)若∠MON=45°,BM=3,BC=12,求 MN 的长度.
相关试题

