【题目】如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F. 
(1)若∠ABE=60°,求∠CDA的度数.
(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.
参考答案:
【答案】
(1)解:∵AC平分∠BCD,AE⊥BC AF⊥CD,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴∠ADF=∠ABE=60°,
∴∠CDA=180°﹣∠ADF=120°;
(2)解:由(1)知:Rt△ABE≌Rt△ADF,
∴FD=BE=1,AF=AE=2,CE=CF=CD+FD=5,
∴BC=CE+BE=6,
∴四边形AECD的面积=△ABC的面积+△ACD的面积= ![]() +
+ ![]() =
= ![]() =10.
=10.
【解析】(1)由角平分线的性质定理证得AE=AF,进而证出△ABE≌△ADF,再得出∠CDA=120°;(2)四边形AECD的面积化为△ABC的面积+△ACD的面积,根据三角形面积公式求出结论.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子是完全平方式的是( )
A.a2+2ab﹣b2B.a2+2a+1C.a2+ab+b2D.a2+2a﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2-9与x2-6x+9有相同的因式是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数a、b满足a+b=5,a2b+ab2=-10,则ab的值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C是数轴上三点,点C表示的数为9,BC=6,AB=18.
(1)数轴上点A表示的数为______;点B表示的数为______.
(2)若动点P从A出发沿数轴匀速向右运动,速度为每秒6个单位,M为AP中点,设运动时间为t(t>0)秒,则数轴上点M表示的数为____________;(用含t的式子表示)
(3)若动点P、Q同时从A、C出发,分别以6个单位长度每秒和3个单位长度每秒的速度,沿数轴匀速向右运动.N在线段PQ上,且
 ,设运动时间为t(t>0)秒,则数轴上点N表示的数为____________(用含t的式子表示).
,设运动时间为t(t>0)秒,则数轴上点N表示的数为____________(用含t的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
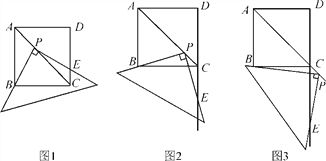
(1)如图1,将直角三角板的直角顶点P放在正方形ABCD的对角线AC上,一条直角边经过点B,另一条直角边交边DC于点E,线段PB和线段PE相等吗?请证明;
问题探究
(2)如图2,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;
问题解决
(3)继续移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2a(b2c3)2·(-2a2b)3;
(2)(2x-1)2-x(4x-1);
(3)632+2×63×37+372.(用简便方法)
相关试题

