【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点,则△AOE与△BMF的面积比为 . 
参考答案:
【答案】3:4
【解析】解:设AB=AC=m,则BM= ![]() m, ∵O是两条对角线的交点,
m, ∵O是两条对角线的交点,
∴OA=OC= ![]() AC=
AC= ![]() m,
m,
∵∠B=30°,AB=AC,
∴∠ACB=∠B=30°,
∵EF⊥AC,
∴cos∠ACB= ![]() ,即cos30°=
,即cos30°= ![]() ,
,
∴FC= ![]() m,
m,
∵AE∥FC,
∴∠EAC=∠FCA,
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,
∴AE=FC= ![]() m,
m,
∴OE= ![]() AE=
AE= ![]() m,
m,
∴S△AOE= ![]() OAOE=
OAOE= ![]() ×
× ![]() ×
× ![]() m=
m= ![]() m2 ,
m2 ,
作AN⊥BC于N,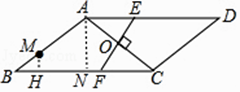
∵AB=AC,
∴BN=CN= ![]() BC,
BC,
∵BN= ![]() AB=
AB= ![]() m,
m,
∴BC= ![]() m,
m,
∴BF=BC﹣FC= ![]() m﹣
m﹣ ![]() m=
m= ![]() m,
m,
作MH⊥BC于H,
∵∠B=30°,
∴MH= ![]() BM=
BM= ![]() m,
m,
∴S△BMF= ![]() BFMH=
BFMH= ![]() ×
× ![]() m×
m× ![]() m=
m= ![]() m2 ,
m2 ,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是3:4.
【考点精析】根据题目的已知条件,利用平行四边形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的大致图象是( )
的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面三个命题: ①若
 是方程组
是方程组  的解,则a+b=1或a+b=0;
的解,则a+b=1或a+b=0;
②函数y=﹣2x2+4x+1通过配方可化为y=﹣2(x﹣1)2+3;
③最小角等于50°的三角形是锐角三角形,
其中正确命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B两城市相距100km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:
 ≈1.732,
≈1.732,  ≈1.414)
≈1.414)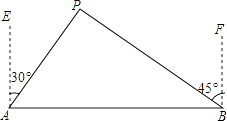
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|2﹣ |﹣
|﹣  (
(  ﹣
﹣  )+
)+  ;
;
(2)先化简,再求值: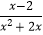 ÷
÷ 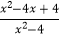 +
+ 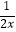 ,其中x=﹣
,其中x=﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.

(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.
相关试题

