搜索
【题目】正方形ABCD中，F是AB上一点，H是BC延长线上一点，连接FH，将△FBH沿FH翻折，使点B的对应点E落在AD上，EH与CD交于点G，连接BG交FH于点M，当GB平分∠CGE时，BM=2
，AE=8，则ED=______．
参考答案：
【答案】4．
【解析】解：如图，过B作BP⊥EH于P，连接BE，交FH于N，则∠BPG=90°．∵四边形ABCD是正方形，∴∠BCD=∠ABC=∠BAD=90°，AB=BC，∴∠BCD=∠BPG=90°．∵GB平分∠CGE，∴∠EGB=∠CGB．又∵BG=BG，∴△BPG≌△BCG，∴∠PBG=∠CBG，BP=BC，∴AB=BP．∵∠BAE=∠BPE=90°，BE=BE，∴Rt△ABE≌Rt△PBE（HL），∴∠ABE=∠PBE，∴∠EBG=∠EBP+∠GBP=
∠ABC=45°，由折叠得：BF=EF，BH=EH，∴FH垂直平分BE，∴△BNM是等腰直角三角形．∵BM=2
，∴BN=NM=2
，∴BE=4
．∵AE=8，∴Rt△ABE中，AB=
=12，∴AD=12，∴DE=12﹣8=4．故答案为：4．
-
科目： 来源： 题型：
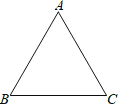
查看答案和解析>>【题目】如图，在等边三角形ABC中，AB=5，在AB边上有一点P，过点P作PM⊥BC，垂足为M，过点M作MN⊥AC，垂足为N，过点N作NQ⊥AB，垂足为Q．当PQ=1时，BP=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线的不等式为y=﹣x2+6x+c．
（1）若抛物线与x轴有交点，求c的取值范围；
（2）设抛物线与x轴两个交点的横坐标分别为x1 ， x2 ． 若x12+x22=26，求c的值．
（3）若P，Q是抛物线上位于第一象限的不同两点，PA，QB都垂直于x轴，垂足分别为A，B，且△OPA与△OQB全等．求证：c＞﹣
．
-
科目： 来源： 题型：
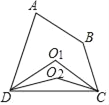
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A+∠B=200°，作∠ADC、∠BCD的平分线交于点O1称为第1次操作，作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作，作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作，…，则第5次操作后∠CO5D的度数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是圆O的直径，C，D是圆O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F．则下列结论：
①AD⊥BD；②∠AOC=∠ABC；③CB平分∠ABD；④AF=DF；⑤BD=2OF．
其中一定成立的是（ ）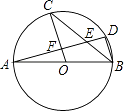
A.①③⑤
B.②③④
C.②④⑤
D.①③④⑤ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是 ．
相关试题
