【题目】如图所示,已知A(![]() ,
, ![]() ),B(2,
),B(2, ![]() )为反比例函数y=
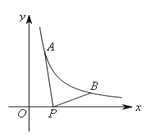
)为反比例函数y=![]() 图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
参考答案:
【答案】D
【解析】试题分析:∵把A(![]() ,y1),B(2,y2)代入反比例函数
,y1),B(2,y2)代入反比例函数![]() 得:y1=2,y2=
得:y1=2,y2=![]() ,
,
∴A(![]() ,2),B(2,
,2),B(2, ![]() ),
),
∵在△ABP中,由三角形的三边关系定理得:|AP﹣BP|<AB,
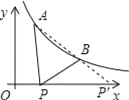
∴延长AB交x轴于P′,当P在P′点时,PA﹣PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得: 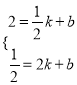 ,
,
解得:k=﹣1,b=![]() ,
,
∴直线AB的解析式是y=﹣x+![]() ,
,
当y=0时,x=![]() ,
,
即P(![]() ,0),
,0),
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知A(﹣1,2),B(﹣3,1)C(0,﹣1)
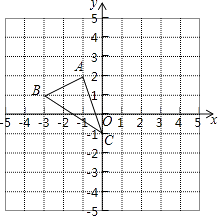
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1
(2)若将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 .
(3)AC的长等于 , △ABC的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,2)与点B(m,2)关于y轴对称,则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展好大课间活动,欲购买单价为20元的排球和单价为80元的篮球共100个.
(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6620元,并且篮球数不少于排球数的3倍,那么有哪几种购买方案?
(3)从节约开支的角度来看,你认为采用哪种方案更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (ab3)2=a2b6 B. a2·a3=a6 C. (a+b)(a-2b)=a2-2b2 D. 5a-2a=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+1)2=9,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣b2)3的结果正确的是( )
A. ﹣b6B. b6C. b5D. ﹣b5
相关试题

