【题目】如图,在长方形ABCD中,DC=5 cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设落点为F,若△ABF的面积为30 cm2,求△ADE的面积.

参考答案:
【答案】S△ADE=16.9 cm2.
【解析】
根据题意和折叠的性质可先求出BF,再根据勾股定理求出DE,然后计算三角形ADE的面积即可
由折叠可知AD=AF,DE=EF.
由S△ABF=![]() BF·AB=30 cm2,
BF·AB=30 cm2,
AB=DC=5 cm,得BF=12 cm.
在Rt△ABF中,由勾股定理,得AF=13 cm,所以BC=AD=AF=13 cm.
设DE=x cm,则EC=(5-x)cm,
EF=x cm,FC=13-12=1(cm).
在Rt△ECF中,由勾股定理,得EC2+FC2=EF2,即(5-x)2+12=x2,解得x=![]() .
.
所以S△ADE=![]() AD·DE=
AD·DE=![]() ×13×
×13×![]() =16.9 (cm2).
=16.9 (cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有5张看上去无差别的卡片,上面分别写着0,π,
 ,
,  ,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
A.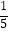
B.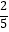
C.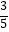
D.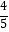
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
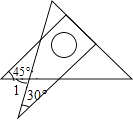
A.75°
B.65°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究
图(1)
定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
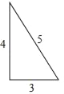
小东用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分用24根火柴棒摆出直角“整数三角形”;
小军受到小东、小颖的启发,用30根火柴棒摆出直角“整数三角形”;
(1)请你画出小颖和小军摆出的直角“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①摆出一个等腰“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为菱形ABCD的BC边的中点,动点F在对角线AC上运动,连接BF、EF,设AF=x,△BEF的周长为y,那么能表示y与x的函数关系的大致图象是( )
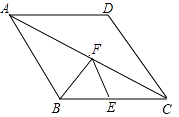
A.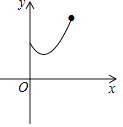
B.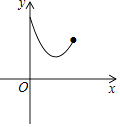
C.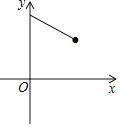
D.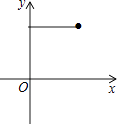
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
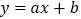 和
和 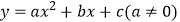 同一直角坐标系内的图象是( )
同一直角坐标系内的图象是( )
A.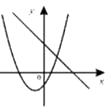
B.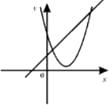
C.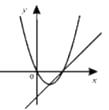
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
(1)求△ABC的周长;
(2)判断△ABC的形状并加以证明.
相关试题

