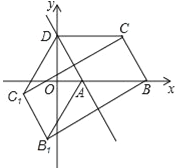
【题目】如图,已知ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作ABCD关于直线AD的对称图形AB1C1D.
(1)若m=3,试求四边形CC1B1B面积S的最大值;
(2)若点B1恰好落在y轴上,试求![]() 的值.
的值.
参考答案:
【答案】(1)9;(2)![]() .
.
【解析】
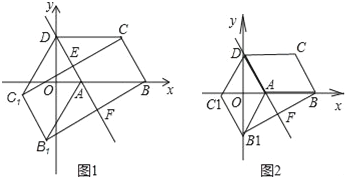
试题分析:(1)如图1,易证SBCEF=SBCDA=SB1C1DA=SB1C1EF,从而可得SBCC1B1=2SBCDA=![]() ,根据二次函数的最值性就可解决问题;
,根据二次函数的最值性就可解决问题;
(2)如图2,易证△AOD∽△B1OB,根据相似三角形的性质可得OB1=![]() ,然后在Rt△AOB1中运用勾股定理就可解决问题.
,然后在Rt△AOB1中运用勾股定理就可解决问题.
试题解析:(1)如图1,∵ABCD与四边形AB1C1D关于直线AD对称,∴四边形AB1C1D是平行四边形,CC1⊥EF,BB1⊥EF,∴BC∥AD∥B1C1,CC1∥BB1,∴四边形BCEF、B1C1EF是平行四边形,∴SBCEF=SBCDA=SB1C1DA=SB1C1EF,∴SBCC1B1=2SBCDA.
∵A(n,0)、B(m,0)、D(0,2n)、m=3,∴AB=m﹣n=3﹣n,OD=2n,∴SBCDA=ABOD=(3﹣n)2n=![]() =
=![]() ,∴SBCC1B1=2SBCDA=
,∴SBCC1B1=2SBCDA=![]() .
.
∵﹣4<0,∴当n=![]() 时,SBCC1B1最大值为9;
时,SBCC1B1最大值为9;
(2)当点B1恰好落在y轴上,如图2,∵DF⊥BB1,DB1⊥OB,∴∠B1DF+∠DB1F=90°,∠B1BO+∠OB1B=90°,∴∠B1DF=∠OBB1.
∵∠DOA=∠BOB1=90°,∴△AOD∽△B1OB,∴![]() ,∴
,∴![]() ,∴OB1=
,∴OB1=![]() .
.
由轴对称的性质可得AB1=AB=m﹣n.在Rt△AOB1中,![]() ,整理得
,整理得![]() .
.
∵m>0,∴3m﹣8n=0,∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
(1)∠PBC=∠CBD;
(2)
 =ABBD.
=ABBD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,
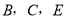 在同一条直线上,连结
在同一条直线上,连结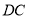 .
.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:
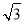 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图8,在
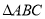 中,
中, 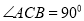 ,
, 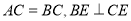 于
于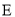 ,
, 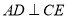 于D.
于D.(1)求证:△ADC≌△CEB. (2)
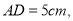
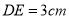 ,求BE的长度.
,求BE的长度.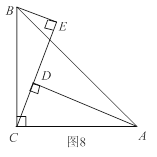
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+2x-4的对称轴是______,顶点坐标是______.
相关试题

