Question

【题目】在平面直角坐标系中，A点的坐标为(0，4)，B点的坐标为(3，0)，C(a，b)为平面直角坐标系内一点，若∠ABC＝90°，且BA＝BC，求ab的值．

Answer 1

【答案】21或3．

【解析】

讨论：当点C在x轴上方．作CD⊥x轴，OA=4，OB=3，由于∠ABC=90°，利用等角的余角相等得到∠BAO=∠CBD，然后根据“AAS”可判断△ABO≌△BCD，则BD=OA=4，CD=OB=3，于是C点坐标为（7，3），得到ab=21；当点C在x轴下方．如图2，作CE⊥x轴，与（1）证明方法一样可证得△ABO≌△BCE，得到BE=OA=4，CE=OB=3，则OE=4﹣3=1，所以C点坐标为（﹣1，﹣3），得到ab=3．

当点C在x轴上方．如图1，作CD⊥x轴．

∵A点的坐标为（0，4），B的坐标为（3，0），∴OA=4，OB=3．

∵∠ABC=90°，∴∠ABO+∠CBD=90°，

∵∠ABO+∠BAO=90°，∴∠BAO=∠CBD．

在△ABO和△BCD中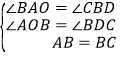，∵，∴△ABO≌△BCD（AAS），∴BD=OA=4，CD=OB=3，∴C点坐标为（7，3），∴ab=7×3=21；

当点C在x轴下方．如图2，作CE⊥x轴，

与（1）证明方法一样可证得△ABO≌△BCE（AAS），∴BE=OA=4，CE=OB=3，∴OE=4﹣3=1，∴C点坐标为（﹣1，﹣3），∴ab=﹣1×（﹣3）=3．

故ab的值为21 或3．