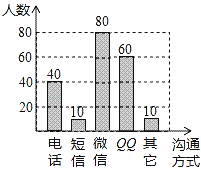
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:

(1)本次调研活动共调研了 名学生,表示“QQ”的扇形圆心角的度数是 度.
(2)请你补充完整条形统计图;
(3)如果该校有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名.
参考答案:
【答案】(1)200,108;(2)见解析;(3)估计最喜欢用“微信”进行沟通的学生有1000名.
【解析】
(1)用最喜欢电话沟通方式的人数除以它所占的百分比得到调研的总人数,用360°乘以最喜欢QQ沟通方式的人数所占的百分比可得到表示“QQ”的扇形圆心角的度数;
(2)求出短信有200×5%=10(名),微信有200-40-10-60-10=80(名),画出条形图即可;
(3)用样本估计总体的思想解决问题即可.
解:(1) 电话占比20%,共40人,所以,共调研了学生数:![]() =200名
=200名
QQ占比:![]() =30%,圆心角:
=30%,圆心角:![]() =108°;
=108°;
(2)短信人数:5%×200=10名,
微信人数:200-40-10-60-10=80,
条形统计图如下:
(3)喜欢用微信沟通所占百分比为:![]() ,
,
![]() =1000名
=1000名
所以,该校共2500名学生中,估计最喜欢用“微信”进行沟通的学生有1000名.
故答案为:(1)200,108;(2)见解析;(3)估计最喜欢用“微信”进行沟通的学生有1000名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有一个四边形ABCD.
(1)分别写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积;
(3)将四边形ABCD先向下平移3个单位长度,再向右平移4个单位长度后得到的四边形A1B1C1D1,画出四边形A1B1C1D1

-
科目: 来源: 题型:
查看答案和解析>>【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
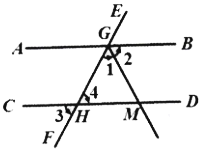
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,(已知)
∴∠4=60°.( )
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+
 ,BC=2
,BC=2 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
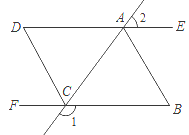
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
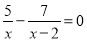
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)参与问卷调查的总人数为 ,扇形统计图中“B”对应的扇形的圆心角度数等于 °;
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
相关试题

