【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
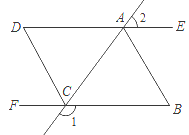
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
参考答案:
【答案】(1)平行,见解析;(2)平行,见解析;(3)平分,见解析.
【解析】
(1)依据∠CAE+∠2=180°,∠1+∠2=180°,即可得到∠1=∠CAE,进而判定DE∥BF;
(2)依据DE∥BF,可得∠B=∠EAB,进而得出∠D=∠EAB,进而判定AB∥CD;
(3)依据CD平分∠ACF,可得∠FCD=∠DCA,再根据平行线的性质,即可得到∠FCD=∠D=∠EAB,∠DCA=∠CAB,进而得出∠CAB=∠EAB,即AB平分∠CAE.
解: (1)平行,
因为∠CAE+∠2=180°,
∠1+∠2=180°,
所以,∠1=∠CAE,
所以,DE∥BF;
(2)平行,
由(1)得DE∥BF,
所以,∠B=∠EAB,
因为∠B=∠D,
所以,∠EAB=∠D,
所以,AB∥CD;
(3)平分,
∵CD平分∠ACF,
∴∠FCD=∠DCA,
又∵DE∥BF,AB∥CD,
∴∠FCD=∠D=∠EAB,∠DCA=∠CAB,
∴∠CAB=∠EAB,
即AB平分∠CAE.
故答案为:(1)平行,见解析;(2)平行,见解析;(3)平分,见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
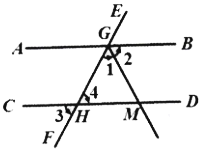
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,(已知)
∴∠4=60°.( )
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+
 ,BC=2
,BC=2 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:

(1)本次调研活动共调研了 名学生,表示“QQ”的扇形圆心角的度数是 度.
(2)请你补充完整条形统计图;
(3)如果该校有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
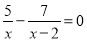
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)参与问卷调查的总人数为 ,扇形统计图中“B”对应的扇形的圆心角度数等于 °;
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让孩子们了解更多的海洋文化知识,市海洋局购买了一批有关海洋文化知识的科普书籍和绘本故事书籍捐赠给市里的几所中小学校.经了解,以两类书的平均单价计算,30本科普书籍和50本绘本故事书籍共需2100元;20本科普书籍比10本绘本故事书籍多100元.
(1)求平均每本科普书籍和绘本故事书籍各是多少元.
(2)计划每所学校捐赠书籍数目和总费用相同.其中每所学校的科普书籍大于115本,科普书籍比绘本故事书籍多30本,总费用不超过5000元,请求出所有符合条件的购书方案.
相关试题

