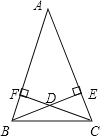
【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A. ① B. ② C. ①② D. ①②③
参考答案:
【答案】D
【解析】结论①:该结论正确,证明如下.
∵BE⊥AC,CF⊥AB,
∴∠AEB=∠AFC=90°.
∵在△ABE和△ACF中,
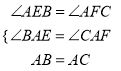 ,
,
∴△ABE≌△ACF (AAS).
结论②:该结论正确,证明如下.
∵△ABE≌△ACF,
∴AE=AF,∠ABE=∠ACF,即∠FBD=∠ECD,
∵AB=AC,AE=AF,
∴AB-AF=AC-AE,即BF=CE,
∵在△BDF和△CDE中,
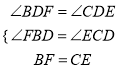 ,
,
∴△BDF≌△CDE (AAS).
结论③:该结论正确,证明如下.

如图,连接AD.
∵△ABE≌△ACF,
∴AE=AF,
∵△BDF≌△CDE,
∴DF=DE,
∵在△AFD和△AED中,
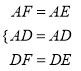 ,
,
∴△AFD≌△AED (SSS),
∴∠FAD=∠EAD,
∴AD平分∠BAC,即点D在∠BAC的平分线上.
综上所述,在本题给出的结论中,正确的是①②③.
故本题应选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学去年通过“废品回收”活动筹集资金用于资助贫困山区中、小学生共27名,其中资助一名中学生的学习费用需要x元,资助一名小学生的学习费用需要y元,各年级学生筹集资金的数额及用其恰好资助中、小学生人数的部分情况如下表:
年级
筹集资金数额
资助贫困中学
资助贫困小学生人数(名)
七年级
5000
2
5
八年级
6000
3
5
九年级
8000
(1)求x,y的值;
(2)九年级学生筹集的资金数解决了其余贫困中、小学生的学习费用,求出九年级学生资助的贫困中、小学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的两直角边长分别是3,4,则它的周长为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?
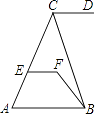
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,M,N分别是OA,OB边上的点,点P在射线OC上,则下列条件中不能说明OC平分∠AOB的是( )
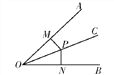
A. PM⊥OA,PN⊥OB,PM=PN B. PM=PN,OM=ON
C. PM⊥OA,PN⊥OB,OM=ON D. PM=PN,∠PMO=∠PNO
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
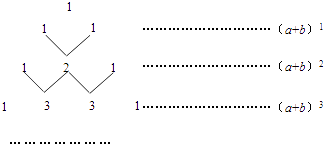
(1)根据上面的规律,则(a+b)5的展开式= .
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>y,则下列不等式成立的是( )
A.x﹣1<y﹣1
B.3x<3y
C.﹣x<﹣y
D.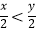
相关试题

