【题目】(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=![]() a,S=
a,S=![]() a2.
a2.
(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②求∠ADB的度数.
③若AD=2,BD=4,求△ABC的面积.
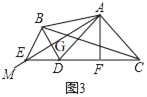
(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.
①求∠EAF的度数;
②若CD=5,BD=2,求BC的长.

参考答案:
【答案】(1)详见解析;(2)①详见解析;②∠ADB=150°;③5![]() +6.;(3)①∠EAF=60°;②BC=
+6.;(3)①∠EAF=60°;②BC=![]() .
.
【解析】
(1)先判断出∠B=30°,BD=![]() BC,再利用三角函数得出BD=
BC,再利用三角函数得出BD=![]() AB,即可得出结论;
AB,即可得出结论;
(2)①先判断出∠DAB=∠EAC,即可得出结论;
②先判断出∠ADB=∠AEC,再求出∠AEC,即可得出结论;
③先利用勾股定理求出EH,AH,再利用勾股定理求出AC2,借助(1)的结论即可得出结论;
(3)①先判断出∠BAE=∠DAE=![]() ∠BAD,∠DAF=∠CAF=
∠BAD,∠DAF=∠CAF=![]() ∠CAD,即可得出∠EAF=
∠CAD,即可得出∠EAF=![]() ∠BAC=60°,
∠BAC=60°,
②先求出DF=![]() CD=2.5,再判断出△BDE是等边三角形,在Rt△AEF中,求出AE=3
CD=2.5,再判断出△BDE是等边三角形,在Rt△AEF中,求出AE=3![]() ,在Rt△DEG中,EF=
,在Rt△DEG中,EF=![]() ,∴AG=AE﹣EG=2
,∴AG=AE﹣EG=2![]() ,在Rt△ABG中,AB=
,在Rt△ABG中,AB=![]() ,即可得出结论.
,即可得出结论.
解:(1)过点A作AD⊥BC于D,
∵AB=AC,∠BAC=120°,
∴BD=![]() BC,∠BAD=60°,
BC,∠BAD=60°,
∴∠B=30°,cosB=![]() ,
,
∴![]() =
=![]() ,
,
∴BD=![]() AB,
AB,
∴BC=![]() AB=
AB=![]() a.
a.
∴S△ABC=![]() BC×AD=
BC×AD=![]() a2;
a2;
(2)
①∵△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,
∴AD=AE,AB=AC,∠DAB=∠EAC,
在△ADB和△AEC中, ,
,
∴△ADB≌△AEC(SAS),
②由①知,△ADB≌△AEC,
∴∠ADB=∠AEC,
在△ADE中,∠DAE=120°,
∴∠AED=30°,
∴∠AEC=150°,
∴∠ADB=150°,
③如图2,过点A作AH⊥CD于H,
∴DH=EH,
在Rt△ADH中,∠ADE=30°,AD=2,
∴AH=1,
∴DH=EH=![]() ,
,
由①知,△ADB≌△AEC,
∴CE=BD=4,
∴CH=CE+EH=4+![]() ,
,
在Rt△ACH中,AC2=AH2+CH2=20+8![]() ,
,
由(1)得,S△ABC=![]() AC2=
AC2=![]() ×(20+8
×(20+8![]() )=5
)=5![]() +6.
+6.
(3)①∵点B与点D关于AM对称,
∴∠BAE=∠DAE=![]() ∠BAD,AB=AD,
∠BAD,AB=AD,
∵AB=AC,
∴AD=AC,
∵AF⊥CE,
∴∠DAF=∠CAF=![]() ∠CAD,
∠CAD,
∴∠EAF=∠DAE+∠DAF=![]() ∠BAD+
∠BAD+![]() ∠CAD=
∠CAD=![]() (∠BAD+∠CAD)=
(∠BAD+∠CAD)=![]() ∠BAC=60°,
∠BAC=60°,
②∵CD=5,
∴DF=![]() CD=2.5,
CD=2.5,
由①知,∠AEF=90°﹣∠EAF=30°,
由对称得,BG=DG=![]() BD=1,∠BED=2∠AEF=60°,BE=DE,
BD=1,∠BED=2∠AEF=60°,BE=DE,
∴△BDE是等边三角形,
∴DE=BD=2,
∴EF=4.5,
在Rt△AEF中,cos∠AEF=![]() ,
,
∴cos30°=![]() ,
,
∴AE=3![]() ,
,
在Rt△DEG中,EF=![]() ,
,
∴AG=AE﹣EG=2![]() ,
,
在Rt△ABG中,AB=![]() =
=![]() ,
,
由(1)知,BC=![]() AB=
AB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣
 ,0),且与反比例函数y=
,0),且与反比例函数y=  (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B. 
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:



因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
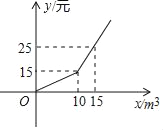
查看答案和解析>>【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y元与每月用水量xm3之间的关系如图所示.
(1)求关于x的函数解析式;
(2)若某用户二、三月份共用水22m3(二月份用水量比三月份用水量多),缴纳水费共35元,则该用户二月份的用水量是多少m3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.

(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=2 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的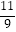 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2 , 线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
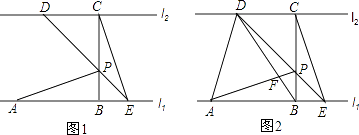
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当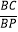 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当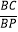 =n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求
=n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求 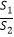 的值.
的值.
相关试题

