【题目】某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).

参考答案:
【答案】(1)旋转木马E处到出口B处的距离为40 m.(2)海洋球D处到出口B处的距离为80 m
【解析】试题分析:(1)在Rt△ABE中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半即可直接求得BE的长;
(2)先求出∠D=30°,设CE=x,则DE=2x,在Rt△CDE中,利用勾股定理列方程求得CE的长,进而求得DE的长,然后利用DB=DE+EB求解.
试题解析:
解:(1)由题意可得,AE=80 m,∠BAE=30°,∠ABE=90°,
∴BE=![]() AE=40 m,
AE=40 m,
即旋转木马E处到出口B处的距离为40 m;
(2∵∠BAE=30°,∠ABE=90°,
∴∠AEB=90°-∠BAE=60°,
∴∠AEB=∠CED=60°,
∴∠D=180°-∠C-∠CED=30°,
设CE=xm,则DE=2xm,
在Rt△CDE中,利用勾股定理得:
342+x2=(2x)2,
解得:x=![]() ,
,
∴DE=2x=![]() ≈40m.
≈40m.
∴DB=DE+BE=40+40=80 m,
即海洋球D处到出口B处的距离为80 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适合于全面调查方式的是( )
A.调查春节联欢晚会的收视率B.调查某班学生的身高情况
C.调查一批节能灯的使用寿命D.调查某批次汽车的抗撞能力
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(x+1,x-2)在x轴上,则点P的坐标是( )
A.(3,0)B.(0,-3)C.(0,-1)D.(-1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,点F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是____.(把所有正确结论的序号都填在横线上)
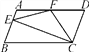
①∠DCF=
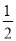 ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】数75000000用科学记数法表示为( )
A.7.5×107B.7.5×106C.75x106D.75×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市为方便相距2 km的A,B两处居民区的交往,修筑一条笔直的公路(即图中的线段AB),经测量,在A处的北偏东60°方向、B处北偏西45°方向的C处有一半径为0.7 km的圆形公园,问计划修筑的公路会不会穿过公园?为什么?

相关试题

